الكسور المتكافئة هي كسور ذات بسط وقواسم مختلفة تمثل نفس القيمة.
\(1/2 = 2/4 = 3/6 = 4/8 \) كسور متكافئة
إذا قسمنا هذه الكسور بعبارات أبسط ، فجميعها تساوي \(\frac{1}{2}\)
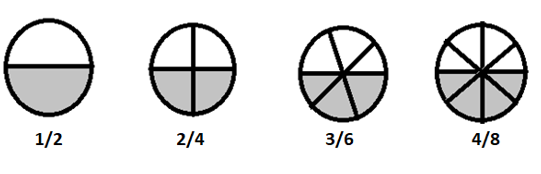
كيفية اختزال الكسر إلى صورة أبسط - اقسم البسط والمقام على عدد صحيح مشترك
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
إذا واصلنا القسمة حتى لا يمكننا المضي قدمًا ، نكون قد بسطنا الكسر.
يمكننا أيضًا ضرب البسط والمقام في العدد نفسه لنصنع كسرًا مكافئًا.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
سيؤدي ضرب أو قسمة البسط والمقام على نفس العدد الصحيح غير الصفري إلى تغيير هذا الكسر إلى كسر مكافئ ، لكنه لن يغير قيمته. قد تبدو الكسور المتكافئة مختلفة ، لكن لها نفس القيمة.
مقارنة الكسر
عند المقارنة بين كسرين لهما مقامات متشابهة ، يكون الكسر الأكبر هو الكسر ذو البسط الأكبر. على سبيل المثال ، ما هو الكسر الأكبر \(^1/_4 \) أو \(^3/_4 \) ؟
بما أن كلاهما له قاسم مشترك ، قارن بين بسط الكسرين:
مثل 3> 1 لذلك \(\frac{3}{4} > \frac{1}{4}\)
وبالمثل ، \(\frac{1}{3} < \frac{2}{3}\)
إذا احتجنا إلى مقارنة الكسور مثل \(^2/_5\) و \(^5/_6 \) . لاحظ أن هذه الكسور لها مقامات مختلفة. سيكون من الأسهل مقارنتهم إذا كان لديهم قواسم مشتركة. حول هذه الكسور إلى كسور متكافئة بحيث يكون لها مقام مشترك:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
الآن كلا الكسرين لهما نفس المقام 30. قارن البسطين في كلا الكسرين. كـ 25> 12 وبالتالي 25/30> 12/30 أي 5/6> 2/5.
إجراء مقارنة الكسور التي لها مقامات مختلفة:
مضاعفات 5 = 5 ، 10 ، 15 ، 20 ، 25 ، 30 ، 35
المضاعفات 0f 6 = 6،12،18،24،30،36
المضاعف المشترك الأصغر للعددين 5 و 6 هو 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)