সমতুল্য ভগ্নাংশ হল বিভিন্ন লব এবং হর সহ ভগ্নাংশ যা একই মানকে প্রতিনিধিত্ব করে।
\(1/2 = 2/4 = 3/6 = 4/8 \) সমতুল্য ভগ্নাংশ
যদি আমরা এই ভগ্নাংশগুলিকে সহজ ভাষায় ভাঙ্গি, তবে এগুলি সবই \(\frac{1}{2}\) এর সমান
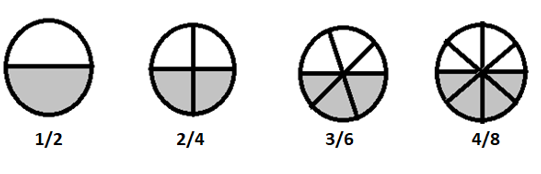
কিভাবে একটি ভগ্নাংশকে সহজ আকারে কমাতে হয় - সাধারণ পূর্ণ সংখ্যা দ্বারা লব এবং হরকে ভাগ করুন
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
যদি আমরা ভাগ করতে থাকি যতক্ষণ না আমরা আরও যেতে না পারি, তাহলে আমরা ভগ্নাংশটিকে সরলীকৃত করেছি।
আমরা একটি সমতুল্য ভগ্নাংশ তৈরি করতে লব এবং হরকে একই সংখ্যা দ্বারা গুণ করতে পারি।
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
আমি
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
লব এবং ভগ্নাংশের হরকে একই অশূন্য পূর্ণ সংখ্যা দ্বারা গুণ বা ভাগ করলে সেই ভগ্নাংশটিকে একটি সমতুল্য ভগ্নাংশে পরিবর্তিত হবে, কিন্তু এটি এর মান পরিবর্তন করবে না । সমতুল্য ভগ্নাংশগুলি আলাদা দেখতে পারে তবে তাদের একই মান রয়েছে।
ভগ্নাংশ তুলনা
দুটি ভগ্নাংশকে অনুরূপ হরগুলির সাথে তুলনা করার সময়, বৃহত্তর ভগ্নাংশটি বৃহত্তর লবের সাথে একটি। উদাহরণস্বরূপ, কোন ভগ্নাংশটি বড় \(^1/_4 \) বা \(^3/_4 \) ?
যেহেতু উভয়েরই একটি সাধারণ হর রয়েছে, উভয় ভগ্নাংশের লব তুলনা করুন:
3 > 1 তাই \(\frac{3}{4} > \frac{1}{4}\)
একইভাবে, \(\frac{1}{3} < \frac{2}{3}\)
যদি আমাদের ভগ্নাংশের তুলনা করতে হয় যেমন \(^2/_5\) এবং \(^5/_6 \) । লক্ষ্য করুন এই ভগ্নাংশের ভিন্ন হর আছে। যদি তাদের সাধারণ হর থাকে তবে তাদের তুলনা করা সহজ হবে। এই ভগ্নাংশগুলিকে সমতুল্য ভগ্নাংশে রূপান্তর করুন যাতে তাদের একটি সাধারণ হর থাকে:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
এখন উভয় ভগ্নাংশের একই হর 30। উভয় ভগ্নাংশের লব তুলনা কর। হিসাবে 25 > 12 তাই 25/30 > 12/30 যেটি 5/6 > 2/5।
ভগ্নাংশের তুলনা করার পদ্ধতি:
5 এর গুণিতক = 5, 10,15,20,25,30,35
বহুগুণ 0f 6 = 6,12,18,24,30,36
5 এবং 6-এর সর্বনিম্ন সাধারণ একাধিক হল 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)