Gleichwertige Brüche sind Brüche mit unterschiedlichen Zählern und Nennern, die denselben Wert darstellen.
\(1/2 = 2/4 = 3/6 = 4/8 \) sind äquivalente Brüche
Wenn wir diese Brüche einfacher brechen, sind sie alle gleich \(\frac{1}{2}\)
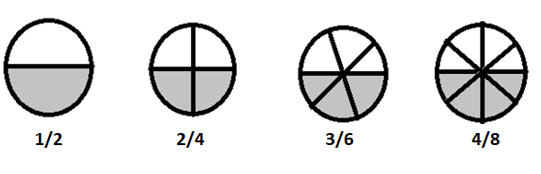
So kürzen Sie einen Bruch auf eine einfachere Form – Dividieren Sie Zähler und Nenner durch eine gemeinsame ganze Zahl
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Wenn wir so lange dividieren, bis es nicht mehr geht, dann haben wir den Bruch vereinfacht.
Wir können auch Zähler und Nenner mit derselben Zahl multiplizieren, um einen äquivalenten Bruch zu bilden.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Das Multiplizieren oder Dividieren des Zählers und des Nenners eines Bruchs mit derselben ganzen Zahl ungleich Null wandelt diesen Bruch in einen äquivalenten Bruch um, ändert jedoch nicht seinen Wert. Äquivalente Brüche können unterschiedlich aussehen, haben aber den gleichen Wert.
Bruch vergleichen
Beim Vergleich zweier Brüche mit gleichem Nenner ist der größere Bruch derjenige mit dem größeren Zähler. Welcher Bruch ist beispielsweise größer \(^1/_4 \) oder \(^3/_4 \) ?
Da beide einen gemeinsamen Nenner haben, vergleichen Sie den Zähler beider Brüche:
da 3 > 1 also \(\frac{3}{4} > \frac{1}{4}\)
Ebenso \(\frac{1}{3} < \frac{2}{3}\)
Wenn wir Brüche wie \(^2/_5\) und \(^5/_6 \) vergleichen müssen. Beachten Sie, dass diese Brüche unterschiedliche Nenner haben. Es wäre einfacher, sie zu vergleichen, wenn sie einen gemeinsamen Nenner hätten. Wandle diese Brüche in äquivalente Brüche um, sodass sie einen gemeinsamen Nenner haben:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Nun haben beide Brüche denselben Nenner 30. Vergleiche die Zähler beider Brüche. Da 25 > 12 also 25/30 > 12/30 ist, ist 5/6 > 2/5.
Verfahren zum Vergleichen von Brüchen mit unterschiedlichen Nennern:
Vielfache von 5 = 5, 10,15,20,25,30,35
Vielfache 0f 6 = 6,12,18,24,30,36
Das kleinste gemeinsame Vielfache von 5 und 6 ist 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)