Equivalent fractions are fractions with different numerators and denominators that represent the same value.
\(1/2 = 2/4 = 3/6 = 4/8 \) are Equivalent fractions
If we break these fractions in simpler terms, they all are equal to \(\frac{1}{2}\)
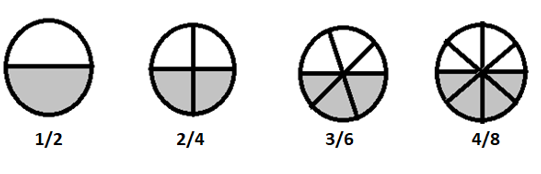
How to reduce a fraction to simpler form – Divide numerator and denominator by common whole number
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
If we keep dividing until we can’t go further, then we have simplified the fraction.
We can also multiply numerator and denominator by the same number to make an equivalent fraction.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Multiplying or dividing the numerator and the denominator of a fraction by the same nonzero whole number will change that fraction into an equivalent fraction, but it will not change its value. Equivalent fractions may look different, but they have the same value.
Comparing Fraction
When comparing two fractions with like denominators, the larger fraction is the one with the greater numerator. For example, which fraction is greater \(^1/_4 \) or \(^3/_4 \) ?
As both have a common denominator, compare the numerator of both the fractions:
as 3 > 1 therefore \(\frac{3}{4} > \frac{1}{4}\)
Similarly, \(\frac{1}{3} < \frac{2}{3}\)
If we need to compare fractions like \(^2/_5\) and \(^5/_6 \) . Notice these fractions have unlike denominators. It would be easier to compare them if they had common denominators. Convert these fractions to equivalent fractions such that they have a common denominator:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Now both the fractions have the same denominator 30. Compare numerators of both the fractions. As 25 > 12 hence 25/30 > 12/30 that is 5/6 > 2/5.
Procedure for comparing fractions having unlike denominators:
Multiples of 5 = 5, 10,15,20,25,30,35
Multiples 0f 6 = 6,12,18,24,30,36
Least Common Multiple of 5 and 6 is 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)