Las fracciones equivalentes son fracciones con diferentes numeradores y denominadores que representan el mismo valor.
\(1/2 = 2/4 = 3/6 = 4/8 \) son fracciones equivalentes
Si dividimos estas fracciones en términos más simples, todas son iguales a \(\frac{1}{2}\)
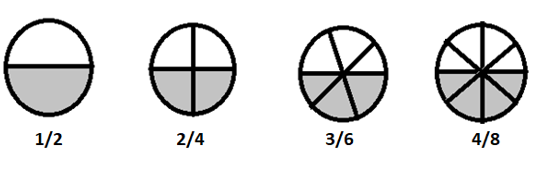
Cómo reducir una fracción a una forma más simple: divide el numerador y el denominador por un número entero común
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Si seguimos dividiendo hasta que no podamos avanzar más, entonces hemos simplificado la fracción.
También podemos multiplicar numerador y denominador por el mismo número para hacer una fracción equivalente.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Multiplicar o dividir el numerador y el denominador de una fracción por el mismo número entero distinto de cero cambiará esa fracción a una fracción equivalente, pero no cambiará su valor. Las fracciones equivalentes pueden verse diferentes, pero tienen el mismo valor.
Fracción de comparación
Cuando se comparan dos fracciones con el mismo denominador, la fracción mayor es la que tiene el numerador mayor. Por ejemplo, ¿qué fracción es mayor \(^1/_4 \) o \(^3/_4 \) ?
Como ambas tienen un denominador común, compara el numerador de ambas fracciones:
como 3 > 1 entonces \(\frac{3}{4} > \frac{1}{4}\)
Del mismo modo, \(\frac{1}{3} < \frac{2}{3}\)
Si necesitamos comparar fracciones como \(^2/_5\) y \(^5/_6 \) . Observa que estas fracciones tienen denominadores diferentes. Sería más fácil compararlos si tuvieran denominadores comunes. Convierta estas fracciones a fracciones equivalentes de manera que tengan un denominador común:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Ahora ambas fracciones tienen el mismo denominador 30. Compara los numeradores de ambas fracciones. Como 25 > 12 por lo tanto 25/30 > 12/30 es decir 5/6 > 2/5.
Procedimiento para comparar fracciones que tienen denominadores diferentes:
Múltiplos de 5 = 5, 10,15,20,25,30,35
Múltiplos 0f 6 = 6,12,18,24,30,36
El mínimo común múltiplo de 5 y 6 es 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)