کسرهای معادل کسری هستند با اعداد و مخرج های متفاوت که مقدار یکسانی را نشان می دهند.
\(1/2 = 2/4 = 3/6 = 4/8 \) کسری معادل هستند
اگر این کسری ها را به صورت ساده تر بشکنیم، همه آنها برابر با \(\frac{1}{2}\) هستند.
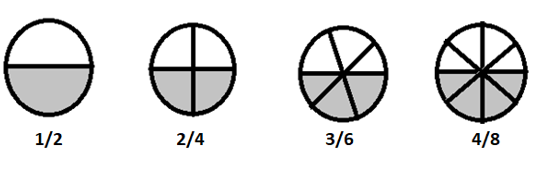
چگونه کسری را به شکل سادهتر کاهش دهیم - صورت و مخرج را بر عدد صحیح تقسیم کنید
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
اگر به تقسیم کردن ادامه دهیم تا زمانی که نتوانیم جلوتر برویم، کسر را ساده کرده ایم.
همچنین می توانیم صورت و مخرج را در یک عدد ضرب کنیم تا کسری معادل بسازیم.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
را
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
ضرب یا تقسیم صورت و مخرج کسری بر همان عدد صحیح غیرصفر، آن کسر را به کسری معادل تبدیل میکند، اما مقدار آن را تغییر نمیدهد . کسرهای معادل ممکن است متفاوت به نظر برسند، اما ارزش یکسانی دارند.
مقایسه کسر
هنگام مقایسه دو کسر با مخرج مشابه، کسری بزرگتر، کسر بزرگتر است. به عنوان مثال، کدام کسری \(^1/_4 \) یا \(^3/_4 \) بزرگتر است؟
از آنجایی که هر دو مخرج مشترک دارند، صورت هر دو کسر را با هم مقایسه کنید:
به عنوان 3 > 1 بنابراین \(\frac{3}{4} > \frac{1}{4}\)
به طور مشابه، \(\frac{1}{3} < \frac{2}{3}\)
اگر نیاز به مقایسه کسری مانند \(^2/_5\) و \(^5/_6 \) داشته باشیم. توجه داشته باشید که این کسرها دارای مخرج های متفاوتی هستند. اگر مخرج مشترک داشتند، مقایسه آنها آسانتر بود. این کسرها را به کسرهای معادل تبدیل کنید تا مخرج مشترک داشته باشند:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
اکنون هر دو کسر مخرج یکسانی دارند 30. شمارنده های هر دو کسر را مقایسه کنید. به عنوان 25 > 12 از این رو 25/30 > 12/30 که 5/6 > 2/5 است.
روش مقایسه کسرهایی که مخرج های متفاوت دارند:
مضرب 5 = 5، 10،15،20،25،30،35
مضرب 0f 6 = 6،12،18،24،30،36
کمترین مضرب مشترک 5 و 6 30 است
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)