Les fractions équivalentes sont des fractions avec des numérateurs et des dénominateurs différents qui représentent la même valeur.
\(1/2 = 2/4 = 3/6 = 4/8 \) sont des fractions équivalentes
Si nous décomposons ces fractions en termes plus simples, elles sont toutes égales à \(\frac{1}{2}\)
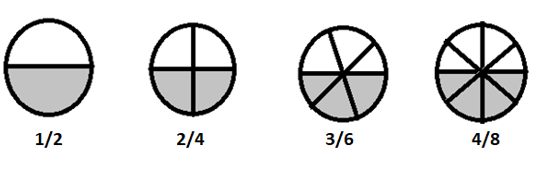
Comment réduire une fraction à une forme plus simple - Diviser le numérateur et le dénominateur par un nombre entier commun
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Si nous continuons à diviser jusqu'à ce que nous ne puissions plus aller plus loin, alors nous avons simplifié la fraction.
Nous pouvons également multiplier le numérateur et le dénominateur par le même nombre pour obtenir une fraction équivalente.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Multiplier ou diviser le numérateur et le dénominateur d'une fraction par le même nombre entier différent de zéro changera cette fraction en une fraction équivalente, mais cela ne changera pas sa valeur. Les fractions équivalentes peuvent sembler différentes, mais elles ont la même valeur.
Comparer des fractions
Lorsque l'on compare deux fractions ayant le même dénominateur, la plus grande fraction est celle qui a le plus grand numérateur. Par exemple, quelle fraction est supérieure à \(^1/_4 \) ou \(^3/_4 \) ?
Comme les deux ont un dénominateur commun, comparez le numérateur des deux fractions :
comme 3 > 1 donc \(\frac{3}{4} > \frac{1}{4}\)
De même, \(\frac{1}{3} < \frac{2}{3}\)
Si nous devons comparer des fractions comme \(^2/_5\) et \(^5/_6 \) . Remarquez que ces fractions ont des dénominateurs différents. Il serait plus facile de les comparer s'ils avaient des dénominateurs communs. Convertissez ces fractions en fractions équivalentes telles qu'elles aient un dénominateur commun :
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Maintenant, les deux fractions ont le même dénominateur 30. Comparez les numérateurs des deux fractions. Comme 25 > 12 donc 25/30 > 12/30 soit 5/6 > 2/5.
Procédure pour comparer des fractions ayant des dénominateurs différents :
Multiples de 5 = 5, 10,15,20,25,30,35
Multiples 0f 6 = 6,12,18,24,30,36
Le plus petit commun multiple de 5 et 6 est 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)