समतुल्य भिन्न भिन्न अंश और हर वाले भिन्न होते हैं जो समान मान का प्रतिनिधित्व करते हैं।
\(1/2 = 2/4 = 3/6 = 4/8 \) समतुल्य भिन्न हैं
यदि हम इन भिन्नों को सरल शब्दों में तोड़ते हैं, तो वे सभी \(\frac{1}{2}\) के बराबर होती हैं
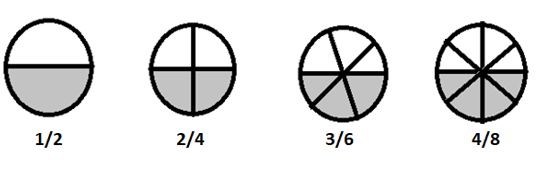
भिन्न को सरल रूप में कैसे कम करें - अंश और हर को सामान्य पूर्ण संख्या से विभाजित करें
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
यदि हम तब तक विभाजित करते रहें जब तक हम आगे नहीं जा सकते, तो हमने भिन्न को सरल बना दिया है।
समान भिन्न बनाने के लिए हम अंश और हर को समान संख्या से गुणा भी कर सकते हैं।
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
मैं
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
किसी भिन्न के अंश और हर को एक ही गैर-शून्य पूर्ण संख्या से गुणा या विभाजित करने पर वह भिन्न एक तुल्य भिन्न में बदल जाएगी, लेकिन इसका मान नहीं बदलेगा। समतुल्य भिन्न भिन्न दिख सकते हैं, लेकिन उनका मान समान है।
भिन्न की तुलना
समान भाजक के साथ दो भिन्नों की तुलना करते समय, बड़ा अंश वह होता है जिसमें बड़ा अंश होता है। उदाहरण के लिए, कौन सा अंश बड़ा है \(^1/_4 \) या \(^3/_4 \) ?
चूंकि दोनों में एक समान भाजक है, दोनों भिन्नों के अंश की तुलना करें:
3 > 1 के रूप में इसलिए \(\frac{3}{4} > \frac{1}{4}\)
इसी तरह, \(\frac{1}{3} < \frac{2}{3}\)
अगर हमें \(^2/_5\) और \(^5/_6 \) जैसे भिन्नों की तुलना करने की आवश्यकता है। ध्यान दें कि इन भिन्नों में विपरीत भाजक हैं। उनकी तुलना करना आसान होगा यदि उनके पास सामान्य भाजक हों। इन भिन्नों को समतुल्य भिन्नों में इस प्रकार परिवर्तित करें कि उनका एक सामान्य हर हो:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
अब दोनों भिन्नों का हर 30 समान है। दोनों भिन्नों के अंशों की तुलना करें। 25> 12 के रूप में 25/30> 12/30 यानी 5/6> 2/5।
भिन्न हर वाले भिन्नों की तुलना करने की प्रक्रिया:
5 के गुणज = 5, 10,15,20,25,30,35
गुणज 0f 6 = 6,12,18,24,30,36
5 और 6 का लघुत्तम समापवर्त्य 30 . है
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)