Ekvivalentni razlomci su razlomci s različitim brojnicima i nazivnicima koji predstavljaju istu vrijednost.
\(1/2 = 2/4 = 3/6 = 4/8 \) su ekvivalentni razlomci
Ako ove razlomke razbijemo jednostavnijim izrazima, svi su jednaki \(\frac{1}{2}\)
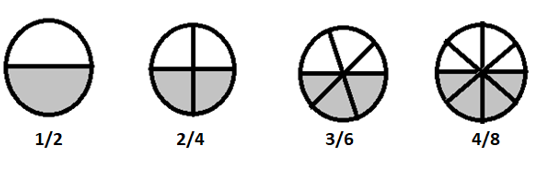
Kako razlomak svesti na jednostavniji oblik – Podijelite brojnik i nazivnik zajedničkim cijelim brojem
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Ako nastavimo s dijeljenjem dok ne možemo ići dalje, onda smo razlomak pojednostavili.
Također možemo pomnožiti brojnik i nazivnik s istim brojem da dobijemo ekvivalentni razlomak.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Množenjem ili dijeljenjem brojnika i nazivnika razlomka istim cijelim brojem različit od nule taj će se razlomak promijeniti u ekvivalentni razlomak, ali neće promijeniti njegovu vrijednost. Ekvivalentni razlomci mogu izgledati drugačije, ali imaju istu vrijednost.
Uspoređivanje razlomka
Kada se uspoređuju dva razlomka sa istim nazivnicima, veći je razlomak s većim brojnikom. Na primjer, koji je razlomak veći \(^1/_4 \) ili \(^3/_4 \) ?
Kako oba imaju zajednički nazivnik, usporedite brojnik oba razlomka:
kao 3 > 1 dakle \(\frac{3}{4} > \frac{1}{4}\)
Slično, \(\frac{1}{3} < \frac{2}{3}\)
Ako trebamo usporediti razlomke kao što su \(^2/_5\) i \(^5/_6 \) . Primijetite da ti razlomci imaju različite nazivnike. Bilo bi ih lakše usporediti da imaju zajedničke nazivnike. Pretvorite ove razlomke u ekvivalentne razlomke tako da imaju zajednički nazivnik:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Sada oba razlomka imaju isti nazivnik 30. Usporedite brojnike oba razlomka. Kao 25 > 12 dakle 25/30 > 12/30 to je 5/6 > 2/5.
Postupak za usporedbu razlomaka koji imaju različite nazivnike:
Višekratnici od 5 = 5, 10,15,20,25,30,35
Višekratnici 0f 6 = 6,12,18,24,30,36
Najmanji zajednički višekratnik 5 i 6 je 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)