Pecahan senilai adalah pecahan dengan pembilang dan penyebut berbeda yang menyatakan nilai yang sama.
\(1/2 = 2/4 = 3/6 = 4/8 \) adalah pecahan senilai
Jika kita memecah pecahan ini menjadi lebih sederhana, semuanya sama dengan \(\frac{1}{2}\)
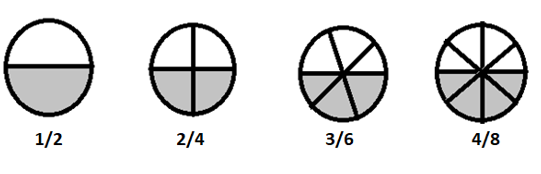
Cara mengurangi pecahan menjadi bentuk yang lebih sederhana – Membagi pembilang dan penyebut dengan bilangan bulat yang sama
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Jika kita terus membagi sampai kita tidak bisa melanjutkan lagi, maka kita telah menyederhanakan pecahan tersebut.
Kita juga bisa mengalikan pembilang dan penyebut dengan angka yang sama untuk membuat pecahan senilai.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Mengalikan atau membagi pembilang dan penyebut suatu pecahan dengan bilangan bulat bukan nol yang sama akan mengubah pecahan tersebut menjadi pecahan yang setara, tetapi tidak akan mengubah nilainya. Pecahan senilai mungkin terlihat berbeda, tetapi memiliki nilai yang sama.
Membandingkan Pecahan
Ketika membandingkan dua pecahan dengan penyebut yang sama, pecahan yang lebih besar adalah pecahan dengan pembilang yang lebih besar. Misalnya, pecahan manakah yang lebih besar \(^1/_4 \) atau \(^3/_4 \) ?
Karena keduanya memiliki penyebut yang sama, bandingkan pembilang kedua pecahan:
sebagai 3 > 1 oleh karena itu \(\frac{3}{4} > \frac{1}{4}\)
Demikian pula, \(\frac{1}{3} < \frac{2}{3}\)
Jika kita perlu membandingkan pecahan seperti \(^2/_5\) dan \(^5/_6 \) . Perhatikan pecahan ini memiliki penyebut yang berbeda. Akan lebih mudah untuk membandingkannya jika mereka memiliki penyebut yang sama. Ubah pecahan ini menjadi pecahan senilai sehingga memiliki penyebut yang sama:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Sekarang kedua pecahan memiliki penyebut yang sama 30. Bandingkan pembilang kedua pecahan tersebut. Karena 25 > 12 maka 25/30 > 12/30 yaitu 5/6 > 2/5.
Prosedur untuk membandingkan pecahan yang memiliki penyebut berbeda:
Kelipatan 5 = 5, 10,15,20,25,30,35
Kelipatan 0f 6 = 6,12,18,24,30,36
Kelipatan Persekutuan Terkecil dari 5 dan 6 adalah 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)