Le frazioni equivalenti sono frazioni con numeratori e denominatori diversi che rappresentano lo stesso valore.
\(1/2 = 2/4 = 3/6 = 4/8 \) sono frazioni equivalenti
Se rompiamo queste frazioni in termini più semplici, sono tutte uguali a \(\frac{1}{2}\)
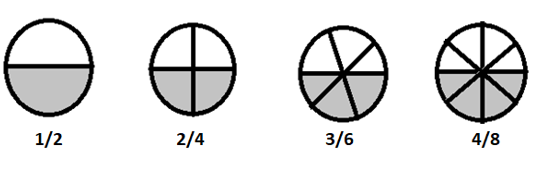
Come ridurre una frazione a una forma più semplice – Dividi numeratore e denominatore per un numero intero comune
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Se continuiamo a dividere finché non possiamo andare oltre, allora abbiamo semplificato la frazione.
Possiamo anche moltiplicare numeratore e denominatore per lo stesso numero per ottenere una frazione equivalente.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Moltiplicando o dividendo il numeratore e il denominatore di una frazione per lo stesso numero intero diverso da zero si trasformerà quella frazione in una frazione equivalente, ma non ne cambierà il valore. Le frazioni equivalenti possono sembrare diverse, ma hanno lo stesso valore.
Frazione a confronto
Quando si confrontano due frazioni con denominatori simili, la frazione maggiore è quella con il numeratore maggiore. Ad esempio, quale frazione è maggiore \(^1/_4 \) o \(^3/_4 \) ?
Poiché entrambi hanno un denominatore comune, confronta il numeratore di entrambe le frazioni:
come 3 > 1 quindi \(\frac{3}{4} > \frac{1}{4}\)
Allo stesso modo, \(\frac{1}{3} < \frac{2}{3}\)
Se dobbiamo confrontare frazioni come \(^2/_5\) e \(^5/_6 \) . Nota che queste frazioni hanno denominatori diversi. Sarebbe più facile confrontarli se avessero denominatori comuni. Converti queste frazioni in frazioni equivalenti tali che abbiano un comune denominatore:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Ora entrambe le frazioni hanno lo stesso denominatore 30. Confronta i numeratori di entrambe le frazioni. Come 25 > 12 quindi 25/30 > 12/30 cioè 5/6 > 2/5.
Procedura per confrontare frazioni con denominatori diversi:
Multipli di 5 = 5, 10,15,20,25,30,35
Multipli 0f 6 = 6,12,18,24,30,36
Il minimo comune multiplo di 5 e 6 è 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)