等価分数は、同じ値を表す異なる分子と分母を持つ分数です。
\(1/2 = 2/4 = 3/6 = 4/8 \)同等の分数です
これらの分数をより簡単な言葉で割ると、それらはすべて\(\frac{1}{2}\)に等しくなります。
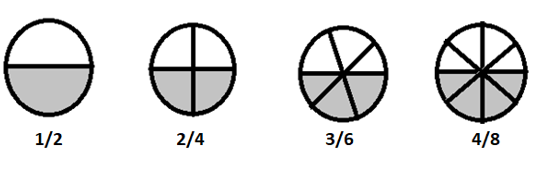
分数をより単純な形に減らす方法 – 分子と分母を共通の整数で割る
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
先に進めなくなるまで割り続けると、分数が単純化されたことになります。
分子と分母に同じ数を掛けて、同等の分数を作ることもできます。
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
な
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
分数の分子と分母をゼロ以外の同じ整数で乗算または除算すると、その分数は同等の分数に変わりますが、その値は変わりません。同等の分数は異なって見える場合がありますが、値は同じです。
分数の比較
分母が似ている 2 つの分数を比較すると、分子が大きい方の分数が大きくなります。たとえば、 \(^1/_4 \)と\(^3/_4 \)のどちらが大きいですか?
両方に共通の分母があるため、両方の分数の分子を比較します。
3 > 1 なので\(\frac{3}{4} > \frac{1}{4}\)
同様に、 \(\frac{1}{3} < \frac{2}{3}\)
\(^2/_5\)と\(^5/_6 \)のような分数を比較する必要がある場合。これらの分数は分母が異なることに注意してください。共通点があれば比較しやすいです。これらの分数を、共通の分母を持つように同等の分数に変換します。
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
これで、両方の分数の分母が同じ 30 になりました。両方の分数の分子を比較してください。 25 > 12 なので、25/30 > 12/30、つまり 5/6 > 2/5 です。
分母が異なる分数を比較する手順:
5 の倍数 = 5、10、15、20、25、30、35
倍数 0f 6 = 6,12,18,24,30,36
5と6の最小公倍数は30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)