ညီမျှသောအပိုင်းကိန်းများသည် တူညီသောတန်ဖိုးကိုကိုယ်စားပြုသည့် မတူညီသော ပိုင်းဝေများနှင့် ပိုင်းခြေများပါရှိသော အပိုင်းများဖြစ်သည်။
\(1/2 = 2/4 = 3/6 = 4/8 \) အပိုင်းများသည် ညီမျှသည်
ဤအပိုင်းများကို ပိုမိုရိုးရှင်းသောဝေါဟာရများဖြင့် ချိုးဖျက်ပါက၊ ၎င်းတို့အားလုံးသည် \(\frac{1}{2}\) နှင့် ညီမျှသည်
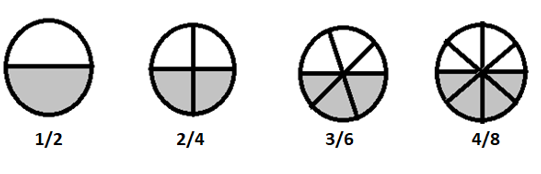
အပိုင်းကိန်းကို ပိုမိုရိုးရှင်းသောပုံစံသို့ လျှော့ချနည်း - ပိုင်းဝေနှင့် ပိုင်းခြေကို ဘုံကိန်းလုံးဖြင့် ပိုင်းပါ။
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
အကယ်၍ ကျွန်ုပ်တို့ ဆက်၍မသွားနိုင်တော့သည့်တိုင်အောင် ခွဲဝေနေပါက၊ ကျွန်ုပ်တို့သည် အပိုင်းများကို ရိုးရှင်းအောင်ပြုလုပ်ထားသည်။
ညီမျှသောအပိုင်းကိန်းတစ်ခုရရန် တူညီသောကိန်းဂဏာန်းဖြင့် ပိုင်းဝေနှင့် ပိုင်းခြေကိုလည်း မြှောက်နိုင်သည်။
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
့
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
ပိုင်းဝေကို မြှောက်ခြင်း သို့မဟုတ် ပိုင်းဝေခြင်းနှင့် အပိုင်းအစတစ်ခု၏ ပိုင်းခြေကို တူညီသောမဟုတ်သော ဂဏန်းတစ်ခုလုံးဖြင့် ပေါင်းခြင်းသည် အဆိုပါအပိုင်းကိန်းကို ညီမျှသောအပိုင်းတစ်ခုအဖြစ်သို့ ပြောင်းလဲစေမည်ဖြစ်ပြီး ၎င်း၏တန်ဖိုးကို ပြောင်းလဲ မည်မဟုတ်ပါ ။ ညီမျှသောအပိုင်းကိန်းများသည် ကွဲပြားသော်လည်း ၎င်းတို့တွင် တူညီသောတန်ဖိုးရှိသည်။
အပိုင်းအစ နှိုင်းယှဉ်ခြင်း။
အပိုင်းကိန်းနှစ်ခုကို ပိုင်းခြေများကဲ့သို့ နှိုင်းယှဉ်သောအခါ၊ ပိုကြီးသောအပိုင်းသည် ပိုကြီးသောပိုင်းဝေနှင့် တစ်ခုဖြစ်သည်။ ဥပမာ၊ ဘယ်အပိုင်းကိန်းက ပိုကြီးလဲ \(^1/_4 \) သို့မဟုတ် \(^3/_4 \) ?
နှစ်ခုလုံးတွင် တူညီသော ပိုင်းခြေရှိသဖြင့် အပိုင်းကိန်းနှစ်ခုလုံး၏ ပိုင်းဝေကို နှိုင်းယှဉ်ပါ-
3 > 1 ထို့ကြောင့် \(\frac{3}{4} > \frac{1}{4}\)
အလားတူ၊ \(\frac{1}{3} < \frac{2}{3}\)
\(^2/_5\) နှင့် \(^5/_6 \) ကဲ့သို့သော အပိုင်းအစများကို နှိုင်းယှဉ်ရန် လိုအပ်ပါက၊ ဤအပိုင်းကိန်းများသည် ပိုင်းခြေများနှင့်မတူကြောင်း သတိပြုပါ။ ဘုံပိုင်းခြေများရှိပါက ၎င်းတို့ကို နှိုင်းယှဉ်ရန် ပိုမိုလွယ်ကူမည်ဖြစ်သည်။ ဤအပိုင်းများကို ၎င်းတို့တွင် ဘုံပိုင်းခြေရှိသည့် ညီမျှသောအပိုင်းများအဖြစ် ပြောင်းပါ-
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
ယခု အပိုင်းကိန်းနှစ်ခုစလုံးတွင် တူညီသောပိုင်းခြေ 30 ရှိသည်။ အပိုင်းကိန်းနှစ်ခုစလုံး၏ ပိုင်းဝေများကို နှိုင်းယှဉ်ပါ။ 25 > 12 ဖြစ်သောကြောင့် 25/30 > 12/30 ဖြစ်သည့် 5/6 > 2/5 ဖြစ်သည်။
ပိုင်းခြေများနှင့်မတူသော အပိုင်းကိန်းများကို နှိုင်းယှဉ်ရန် လုပ်ထုံးလုပ်နည်း-
5 = 5၊ 10၊15၊20၊25၊30၊35
အမြောက်များ 0f 6 = 6,12,18,24,30,36
5 နှင့် 6 ၏ အနည်းစုသည် 30 ဖြစ်သည်။
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)