समतुल्य अंशहरू भिन्न संख्याहरू र भाजकहरू भएका भिन्नहरू हुन् जसले समान मानलाई प्रतिनिधित्व गर्दछ।
\(1/2 = 2/4 = 3/6 = 4/8 \) बराबर अंशहरू हुन्
यदि हामीले यी अंशहरूलाई सरल शब्दहरूमा तोड्यौं भने, तिनीहरू सबै \(\frac{1}{2}\) बराबर हुन्छन्।
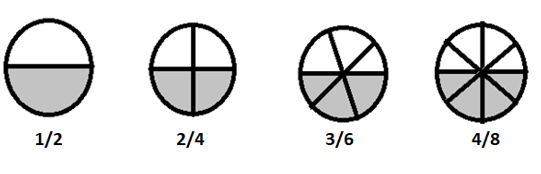
अंशलाई सरल रूपमा कसरी घटाउने - अंश र भाजकलाई सामान्य पूर्ण संख्याले विभाजन गर्नुहोस्
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
यदि हामी भाग गर्न जारी राख्छौं जबसम्म हामी अगाडि जान सक्दैनौं, तब हामीले अंशलाई सरलीकृत गरेका छौं।
हामी बराबर अंश बनाउनको लागि अंक र भाजकलाई समान संख्याले गुणन गर्न सक्छौं।
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
को
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
अंशको अंश र भाजकलाई समान शून्य पूर्ण संख्याले गुणन वा भाग गर्दा त्यो अंशलाई बराबर अंशमा परिवर्तन हुनेछ, तर यसले यसको मान परिवर्तन गर्दैन । समान भिन्नहरू फरक देखिन सक्छन्, तर तिनीहरूको समान मूल्य छ।
अंश तुलना गर्दै
दुई भिन्नहरूलाई समान भाजकहरूसँग तुलना गर्दा, ठूलो अंश ठूलो अंश भएको एउटा हो। उदाहरणका लागि, कुन अंश ठूलो हो \(^1/_4 \) वा \(^3/_4 \) ?
दुबैको साझा भाजक भएको हुनाले, दुबै भिन्नहरूको अंश तुलना गर्नुहोस्:
3 > 1 त्यसैले \(\frac{3}{4} > \frac{1}{4}\)
त्यस्तै, \(\frac{1}{3} < \frac{2}{3}\)
यदि हामीले भिन्नहरू जस्तै \(^2/_5\) र \(^5/_6 \) तुलना गर्न आवश्यक छ भने। ध्यान दिनुहोस् कि यी अंशहरूमा भिन्नताहरू छन्। यदि तिनीहरूसँग समान डिनोमिनेटरहरू छन् भने तिनीहरूलाई तुलना गर्न सजिलो हुनेछ। यी भिन्नहरूलाई समान भिन्नहरूमा रूपान्तरण गर्नुहोस् जस्तै कि तिनीहरूसँग साझा भाजक छ:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
अब दुबै भिन्नहरूको एउटै भाजक 30 छ। दुबै भिन्नहरूको संख्याहरू तुलना गर्नुहोस्। 25 > 12 त्यसैले 25/30 > 12/30 जुन 5/6 > 2/5 हो।
भिन्न भिन्नता भएका भिन्नहरू तुलना गर्ने प्रक्रिया:
५ को गुणन = ५, १०,१५,२०,२५,३०,३५
गुणन 0f 6 = 6,12,18,24,30,36
५ र ६ को न्यूनतम सामान्य गुणन ३० हो
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)