Equivalente breuken zijn breuken met verschillende tellers en noemers die dezelfde waarde vertegenwoordigen.
\(1/2 = 2/4 = 3/6 = 4/8 \) zijn equivalente breuken
Als we deze breuken in eenvoudiger bewoordingen breken, zijn ze allemaal gelijk aan \(\frac{1}{2}\)
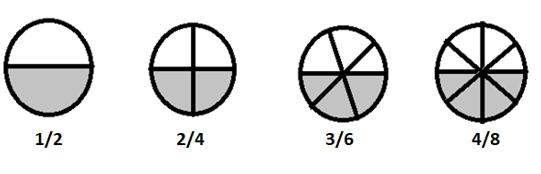
Hoe een breuk te verkleinen tot een eenvoudigere vorm - Deel teller en noemer door gewoon geheel getal
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Als we blijven delen tot we niet verder kunnen, dan hebben we de breuk vereenvoudigd.
We kunnen teller en noemer ook vermenigvuldigen met hetzelfde getal om een equivalente breuk te maken.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Vermenigvuldigen of delen van de teller en de noemer van een breuk met hetzelfde geheel getal dat niet nul is, zal die breuk veranderen in een equivalente breuk, maar de waarde ervan verandert niet . Equivalente breuken kunnen er anders uitzien, maar ze hebben dezelfde waarde.
breuk vergelijken
Bij het vergelijken van twee breuken met gelijke noemers, is de grotere breuk degene met de grotere teller. Welke breuk is bijvoorbeeld groter \(^1/_4 \) of \(^3/_4 \) ?
Aangezien beide een gemeenschappelijke noemer hebben, vergelijkt u de teller van beide breuken:
als 3 > 1 dus \(\frac{3}{4} > \frac{1}{4}\)
Evenzo geldt \(\frac{1}{3} < \frac{2}{3}\)
Als we breuken zoals \(^2/_5\) en \(^5/_6 \) moeten vergelijken. Merk op dat deze breuken ongelijke noemers hebben. Het zou gemakkelijker zijn om ze te vergelijken als ze gemeenschappelijke noemers hadden. Converteer deze breuken naar equivalente breuken zodat ze een gemeenschappelijke noemer hebben:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Nu hebben beide breuken dezelfde noemer 30. Vergelijk tellers van beide breuken. Als 25 > 12 dus 25/30 > 12/30 is dat 5/6 > 2/5.
Procedure voor het vergelijken van breuken met ongelijke noemers:
Veelvouden van 5 = 5, 10,15,20,25,30,35
Veelvouden 0f 6 = 6,12,18,24,30,36
Kleinste gemene veelvoud van 5 en 6 is 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)