Ułamki równoważne to ułamki o różnych licznikach i mianownikach, które reprezentują tę samą wartość.
\(1/2 = 2/4 = 3/6 = 4/8 \) to ułamki równoważne
Jeśli podzielimy te ułamki w prostszy sposób, wszystkie będą równe \(\frac{1}{2}\)
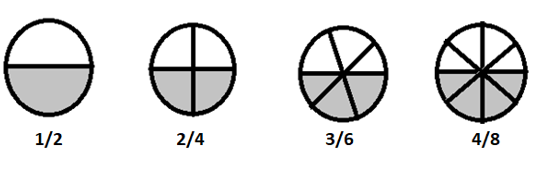
Jak sprowadzić ułamek do prostszej postaci – Podziel licznik i mianownik przez wspólną liczbę całkowitą
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Jeśli dzielimy dalej, aż nie możemy iść dalej, to uprościliśmy ułamek.
Możemy również pomnożyć licznik i mianownik przez tę samą liczbę, aby otrzymać ułamek równoważny.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Mnożenie lub dzielenie licznika i mianownika ułamka przez tę samą niezerową liczbę całkowitą zmieni ten ułamek na ułamek równoważny, ale nie zmieni jego wartości. Równoważne ułamki mogą wyglądać inaczej, ale mają tę samą wartość.
Porównywanie frakcji
Porównując dwa ułamki o podobnych mianownikach, większym ułamkiem jest ten, który ma większy licznik. Na przykład, który ułamek jest większy \(^1/_4 \) czy \(^3/_4 \) ?
Ponieważ oba mają wspólny mianownik, porównaj licznik obu ułamków:
jako 3 > 1 zatem \(\frac{3}{4} > \frac{1}{4}\)
Podobnie, \(\frac{1}{3} < \frac{2}{3}\)
Jeśli musimy porównać ułamki takie jak \(^2/_5\) i \(^5/_6 \) . Zauważ, że te ułamki mają różne mianowniki. Łatwiej byłoby je porównać, gdyby miały wspólny mianownik. Zamień te ułamki na ułamki równoważne tak, aby miały wspólny mianownik:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Teraz oba ułamki mają ten sam mianownik 30. Porównaj liczniki obu ułamków. Skoro 25 > 12, to 25/30 > 12/30, czyli 5/6 > 2/5.
Procedura porównywania ułamków o różnych mianownikach:
Wielokrotności 5 = 5, 10,15,20,25,30,35
Wielokrotności 0f 6 = 6,12,18,24,30,36
Najmniejsza wspólna wielokrotność liczb 5 i 6 to 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)