Frações equivalentes são frações com numeradores e denominadores diferentes que representam o mesmo valor.
\(1/2 = 2/4 = 3/6 = 4/8 \) são frações equivalentes
Se quebrarmos essas frações em termos mais simples, todas elas serão iguais a \(\frac{1}{2}\)
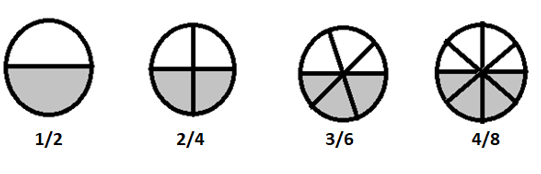
Como reduzir uma fração para uma forma mais simples – Divida o numerador e o denominador por um número inteiro comum
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Se continuarmos dividindo até não podermos ir mais longe, então simplificamos a fração.
Também podemos multiplicar numerador e denominador pelo mesmo número para formar uma fração equivalente.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Multiplicar ou dividir o numerador e o denominador de uma fração pelo mesmo número inteiro diferente de zero transformará essa fração em uma fração equivalente, mas não alterará seu valor. As frações equivalentes podem parecer diferentes, mas têm o mesmo valor.
Comparando Fração
Ao comparar duas frações com denominadores iguais, a fração maior é aquela com o maior numerador. Por exemplo, qual fração é maior \(^1/_4 \) ou \(^3/_4 \) ?
Como ambas têm um denominador comum, compare o numerador de ambas as frações:
como 3 > 1 portanto \(\frac{3}{4} > \frac{1}{4}\)
Da mesma forma, \(\frac{1}{3} < \frac{2}{3}\)
Se precisarmos comparar frações como \(^2/_5\) e \(^5/_6 \) . Observe que essas frações têm denominadores diferentes. Seria mais fácil compará-los se tivessem denominadores comuns. Converta essas frações em frações equivalentes de modo que tenham um denominador comum:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Agora ambas as frações têm o mesmo denominador 30. Compare os numeradores de ambas as frações. Como 25 > 12, portanto, 25/30 > 30/12, que é 5/6 > 2/5.
Procedimento para comparar frações com denominadores diferentes:
Múltiplos de 5 = 5, 10,15,20,25,30,35
Múltiplos 0f 6 = 6,12,18,24,30,36
Mínimo múltiplo comum de 5 e 6 é 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)