Равные дроби — это дроби с разными числителями и знаменателями, которые представляют одно и то же значение.
\(1/2 = 2/4 = 3/6 = 4/8 \) равнозначные дроби
Если мы разобьем эти дроби на более простые термины, все они равны \(\frac{1}{2}\)
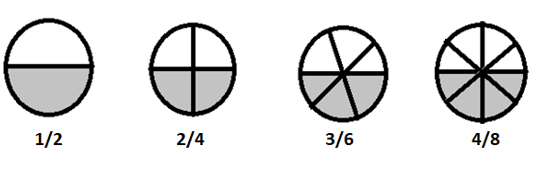
Как привести дробь к более простому виду – Разделить числитель и знаменатель на обычное целое число
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Если мы будем делить до тех пор, пока не сможем продолжить, значит, мы упростили дробь.
Мы также можем умножить числитель и знаменатель на одно и то же число, чтобы получить эквивалентную дробь.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Умножение или деление числителя и знаменателя дроби на одно и то же целое число, отличное от нуля, превратит эту дробь в эквивалентную дробь, но не изменит ее значение. Равные дроби могут выглядеть по-разному, но имеют одинаковое значение.
Сравнение дроби
При сравнении двух дробей с одинаковыми знаменателями больше та дробь, у которой больше числитель. Например, какая дробь больше \(^1/_4 \) или \(^3/_4 \) ?
Поскольку обе дроби имеют общий знаменатель, сравните числитель обеих дробей:
поскольку 3 > 1, следовательно, \(\frac{3}{4} > \frac{1}{4}\)
Точно так же \(\frac{1}{3} < \frac{2}{3}\)
Если нам нужно сравнить дроби, такие как \(^2/_5\) и \(^5/_6 \) . Обратите внимание, что у этих дробей разные знаменатели. Их было бы легче сравнивать, если бы у них были общие знаменатели. Преобразуйте эти дроби в эквивалентные дроби так, чтобы они имели общий знаменатель:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Теперь обе дроби имеют одинаковый знаменатель 30. Сравните числители обеих дробей. Поскольку 25 > 12, следовательно, 25/30 > 12/30, то есть 5/6 > 2/5.
Порядок сравнения дробей с разными знаменателями:
Кратность 5 = 5, 10,15,20,25,30,35
Кратные числа 0f 6 = 6,12,18,24,30,36
Наименьшее общее кратное 5 и 6 равно 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)