Thyesat ekuivalente janë thyesat me numërues dhe emërues të ndryshëm që përfaqësojnë të njëjtën vlerë.
\(1/2 = 2/4 = 3/6 = 4/8 \) janë thyesa ekuivalente
Nëse i thyejmë këto thyesa në terma më të thjeshtë, të gjitha ato janë të barabarta me \(\frac{1}{2}\)
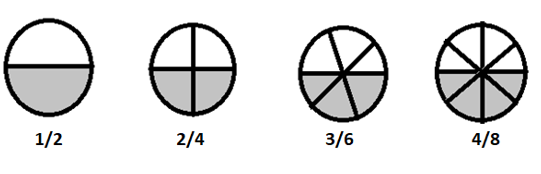
Si të zvogëloni një thyesë në një formë më të thjeshtë - Pjesëtoni numëruesin dhe emëruesin me numrin e plotë të përbashkët
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Nëse vazhdojmë pjesëtimin derisa nuk mund të shkojmë më tej, atëherë e kemi thjeshtuar thyesën.
Ne gjithashtu mund të shumëzojmë numëruesin dhe emëruesin me të njëjtin numër për të bërë një thyesë ekuivalente.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
,
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Shumëzimi ose pjesëtimi i numëruesit dhe i emëruesit të një thyese me të njëjtin numër të plotë jozero do ta ndryshojë atë thyesë në një thyesë ekuivalente, por nuk do të ndryshojë vlerën e saj. Thyesat ekuivalente mund të duken të ndryshme, por ato kanë të njëjtën vlerë.
Krahasimi i thyesës
Kur krahasojmë dy thyesa me emërues të ngjashëm, thyesa më e madhe është ajo me numërues më të madh. Për shembull, cila thyesë është më e madhe \(^1/_4 \) ose \(^3/_4 \) ?
Pasi që të dy kanë një emërues të përbashkët, krahasoni numëruesin e të dy thyesave:
si 3 > 1 pra \(\frac{3}{4} > \frac{1}{4}\)
Në mënyrë të ngjashme, \(\frac{1}{3} < \frac{2}{3}\)
Nëse duhet të krahasojmë thyesat si \(^2/_5\) dhe \(^5/_6 \) . Vini re se këto thyesa kanë emërues të ndryshëm. Do të ishte më e lehtë t'i krahasonim nëse do të kishin emërues të përbashkët. Shndërrojini këto thyesa në thyesa ekuivalente në mënyrë që të kenë një emërues të përbashkët:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Tani të dyja thyesat kanë emërues të njëjtë 30. Krahasoni numëruesit e të dy thyesave. Si 25 > 12 pra 25/30 > 12/30 që është 5/6 > 2/5.
Procedura për krahasimin e thyesave që kanë emërues të ndryshëm:
Shumëfishat e 5 = 5, 10,15,20,25,30,35
Shumëfishat 0f 6 = 6,12,18,24,30,36
Shumëfishi më pak i zakonshëm i 5 dhe 6 është 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)