Ekvivalenta bråk är bråk med olika täljare och nämnare som representerar samma värde.
\(1/2 = 2/4 = 3/6 = 4/8 \) är ekvivalenta bråk
Om vi bryter dessa bråk i enklare termer är de alla lika med \(\frac{1}{2}\)
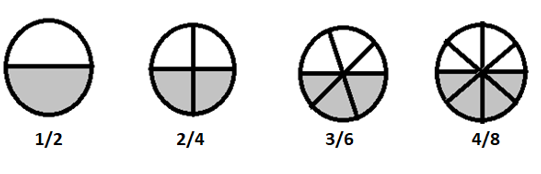
Hur man reducerar ett bråk till enklare form – Dela täljare och nämnare med gemensamt heltal
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Om vi fortsätter att dela tills vi inte kan gå längre, då har vi förenklat bråket.
Vi kan också multiplicera täljare och nämnare med samma tal för att få ett ekvivalent bråk.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
.
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Att multiplicera eller dividera täljaren och nämnaren för ett bråk med samma heltal som inte är noll kommer att ändra det bråket till ett ekvivalent bråk, men det kommer inte att ändra dess värde. Ekvivalenta bråk kan se olika ut, men de har samma värde.
Jämföra fraktion
När man jämför två bråk med lika nämnare, är det större bråket det med den större täljaren. Till exempel, vilken bråkdel är större \(^1/_4 \) eller \(^3/_4 \) ?
Eftersom båda har en gemensam nämnare, jämför täljaren för båda bråken:
som 3 > 1 därför \(\frac{3}{4} > \frac{1}{4}\)
På samma sätt \(\frac{1}{3} < \frac{2}{3}\)
Om vi behöver jämföra bråk som \(^2/_5\) och \(^5/_6 \) . Lägg märke till att dessa bråk har olika nämnare. Det skulle vara lättare att jämföra dem om de hade gemensamma nämnare. Konvertera dessa bråk till ekvivalenta bråk så att de har en gemensam nämnare:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Nu har båda bråken samma nämnare 30. Jämför täljare för båda bråken. Som 25 > 12 därav 25/30 > 12/30 det vill säga 5/6 > 2/5.
Procedur för att jämföra bråk med olika nämnare:
Multiplar av 5 = 5, 10,15,20,25,30,35
Multipel 0f 6 = 6,12,18,24,30,36
Minsta gemensamma multipel av 5 och 6 är 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)