เศษส่วนเทียบเท่าคือเศษส่วนที่มีตัวเศษและตัวส่วนต่างกันซึ่งแทนค่าเดียวกัน
\(1/2 = 2/4 = 3/6 = 4/8 \) เป็นเศษส่วนเทียบเท่า
ถ้าเราแบ่งเศษส่วนเหล่านี้ด้วยคำที่ง่ายกว่า พวกมันทั้งหมดจะเท่ากับ \(\frac{1}{2}\)
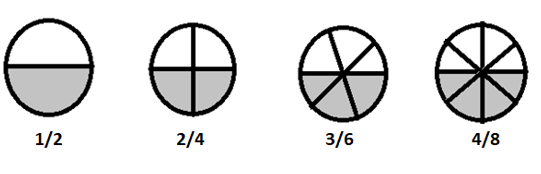
วิธีลดเศษส่วนให้อยู่ในรูปแบบที่ง่ายกว่า – หารตัวเศษและตัวส่วนด้วยจำนวนเต็มร่วมกัน
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
ถ้าเราหารต่อไปจนไปต่อไม่ได้ เราก็ทำให้เศษส่วนลดรูปลงแล้ว
เราสามารถคูณทั้งเศษและส่วนด้วยจำนวนเดียวกันเพื่อสร้างเศษส่วนที่เท่ากันได้
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
การคูณหรือหารตัวเศษและตัวส่วนของเศษส่วนด้วยจำนวนเต็มที่ไม่ใช่ศูนย์เดียวกันจะทำให้เศษส่วนนั้นเป็นเศษส่วนที่เท่ากัน แต่จะ ไม่ เปลี่ยนค่าของเศษส่วนนั้น เศษส่วนเทียบเท่าอาจดูต่างกัน แต่มีค่าเท่ากัน
การเปรียบเทียบเศษส่วน
เมื่อเปรียบเทียบเศษส่วนสองตัวที่มีตัวส่วนเท่ากัน เศษส่วนที่มากกว่าจะเป็นตัวที่มีตัวเศษมากกว่า ตัวอย่างเช่น เศษส่วนใดมากกว่า \(^1/_4 \) หรือ \(^3/_4 \) ?
เนื่องจากทั้งคู่มีตัวส่วนร่วม ให้เปรียบเทียบตัวเศษของเศษส่วนทั้งสอง:
เป็น 3 > 1 ดังนั้น \(\frac{3}{4} > \frac{1}{4}\)
ในทำนองเดียวกัน \(\frac{1}{3} < \frac{2}{3}\)
หากเราต้องเปรียบเทียบเศษส่วนเช่น \(^2/_5\) และ \(^5/_6 \) สังเกตว่าเศษส่วนเหล่านี้ไม่เหมือนตัวส่วน มันจะง่ายกว่าที่จะเปรียบเทียบพวกเขาถ้าพวกเขามีตัวส่วนร่วม แปลงเศษส่วนเหล่านี้เป็นเศษส่วนที่เท่ากันเพื่อให้มีตัวส่วนร่วม:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
ตอนนี้เศษส่วนทั้งสองมีตัวส่วนเท่ากัน 30. เปรียบเทียบตัวเศษของเศษส่วนทั้งสอง เช่น 25 > 12 ดังนั้น 25/30 > 12/30 นั่นคือ 5/6 > 2/5
ขั้นตอนการเปรียบเทียบเศษส่วนที่มีตัวส่วนไม่เหมือนกับตัวส่วน:
ทวีคูณของ 5 = 5, 10,15,20,25,30,35
ทวีคูณ 0f 6 = 6,12,18,24,30,36
ตัวคูณร่วมน้อยของ 5 และ 6 คือ 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)