Рівнозначні дроби — це дроби з різними чисельниками та знаменниками, які представляють однакову величину.
\(1/2 = 2/4 = 3/6 = 4/8 \) є еквівалентними дробами
Якщо розбити ці дроби простіше, усі вони дорівнюватимуть \(\frac{1}{2}\)
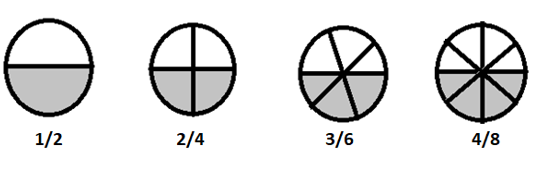
Як звести дріб до простішого вигляду – розділити чисельник і знаменник на звичайне ціле число
\(\frac{2}{4}= \frac{(2⁄2)}{(4⁄2)} = \frac{1}{2}\)
\(\frac{3}{6}= \frac{(3⁄3)}{(6⁄3)} = \frac{1}{2}\)
Якщо ми будемо продовжувати ділити, поки не зможемо піти далі, це означає, що ми спростили дріб.
Ми також можемо помножити чисельник і знаменник на одне й те саме число, щоб отримати еквівалентний дріб.
\(\frac{1\times 2}{2\times2} = \frac{2}{4}\)
\(\frac{2\times2}{4\times2} = \frac{4}{8}\)
\(\frac{1}{2} = \frac{2}{4} = \frac{4}{8}\)
Множення чи ділення чисельника та знаменника дробу на одне й те саме ненульове ціле число перетворить цей дріб на еквівалентний дріб, але не змінить його значення. Еквівалентні дроби можуть виглядати по-різному, але вони мають однакове значення.
Порівняння дробів
Під час порівняння двох дробів з однаковими знаменниками більшим є той, у якого більший чисельник. Наприклад, який дріб більший \(^1/_4 \) чи \(^3/_4 \) ?
Оскільки обидва дроби мають спільний знаменник, порівняйте чисельники обох дробів:
тому що 3 > 1 \(\frac{3}{4} > \frac{1}{4}\)
Подібним чином \(\frac{1}{3} < \frac{2}{3}\)
Якщо нам потрібно порівняти такі дроби \(^2/_5\) і \(^5/_6 \) . Зверніть увагу, що ці дроби мають різні знаменники. Їх було б легше порівнювати, якби вони мали спільні знаменники. Перетворіть ці дроби на еквівалентні дроби, щоб вони мали спільний знаменник:
\(\frac{2\times6}{5\times6} = \frac{12}{30}\)
\(\frac{5\times5}{6\times5} = \frac{25}{30}\)
Тепер обидва дроби мають однаковий знаменник 30. Порівняйте чисельники обох дробів. Оскільки 25 > 12, отже, 25/30 > 12/30, тобто 5/6 > 2/5.
Порядок порівняння дробів з різними знаменниками:
Число, кратне 5 = 5, 10,15,20,25,30,35
Кратні 0f 6 = 6,12,18,24,30,36
Найменше спільне кратне чисел 5 і 6 дорівнює 30
\(\frac{2}{5}\) = \(\frac{2\times6}{5\times6}\) = \(\frac{12}{30}\)
\(\frac{5}{6} = \frac{5\times5}{6\times5} = \frac{25}{30}\)
\(\frac{12}{30} < \frac{25}{30}\)
\(\frac{2}{5} < \frac{5}{6}\)