Un número menor que cero se conoce como número negativo y un número mayor que cero se conoce como número positivo. El cero no es ni positivo ni negativo.
Los números enteros son un subconjunto de los números reales que consisten en todos los números enteros positivos y negativos, incluido el cero. Los números enteros se pueden representar como {...,-3,-2,-1,0,1,2,3,...} y se usan en una variedad de operaciones y aplicaciones matemáticas como contar, medir y describir. cantidades.
Un número negativo se escribe poniendo un signo menos
Los números negativos quedan del cero en la recta numérica. Un número y su opuesto (o negativo) están siempre a la misma distancia del cero. El número negativo -2 está tan a la izquierda del cero como 2 a la derecha del cero.
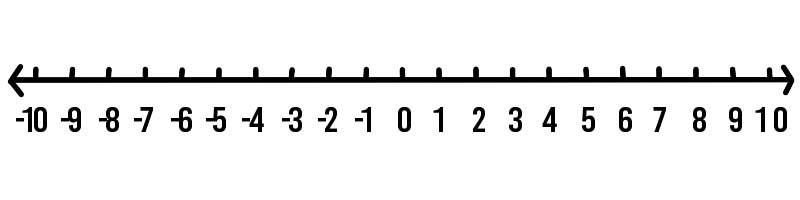
Tomemos un ejemplo del mundo real donde los números negativos se notan fácilmente. Medimos la temperatura para saber qué tan caliente o frío está algo. Consideremos un escenario donde el pronóstico del tiempo predice que mañana hará 4 grados más frío que hoy. La temperatura de hoy es de 3 grados centígrados. ¿Cuál sería la temperatura mañana? Averigüémoslo usando la siguiente recta numérica.
Para saber cuál sería la temperatura de mañana, comience en 3 y retroceda 4 pasos.
Aquí alcanzamos la temperatura de -1. Note que -1 es más frío que 3.
A medida que avanzamos hacia la derecha de la recta numérica, el valor positivo aumenta, del mismo modo que avanzamos hacia la izquierda hacia la recta numérica, aumenta el valor negativo. Pero recuerda que -100 es mucho más pequeño que -1. Los números que aparecen más a la derecha en la recta numérica son más grandes o más grandes, mientras que los números que aparecen más a la izquierda son más pequeños o menos.
Otra situación en la que notas números negativos es en un extracto bancario. Consideremos un escenario en el que depositamos $300 el mes pasado y recibimos un extracto bancario.
Saldo del mes pasado = 300
Gasolinera = -20
Tienda departamental = -50
Saldo total = 230
Los números negativos -20 y -50 representan gastos, mientras que los números positivos representan un crédito o depósito en la cuenta.
Ejemplo 1 : 2 − 5 = ?
Resolvamos esto con una recta numérica.
Mover 5 veces a la izquierda de 2
2 - 5 = -3
Para restar, muévase hacia atrás o hacia la izquierda en la recta numérica.
Ejemplo 2 : -2 + 2 = ?
Comienza con menos 2 y muévete a la derecha 2 veces en la recta numérica.
Llegamos a 0, entonces -2 + 2 = 0.
Para sumar, muévete hacia adelante o hacia la derecha en la recta numérica.
Ejemplo 3 : -2 − 3 = ?
Comienza con menos 2 y muévete a la izquierda 3 veces en la recta numérica.
-2 − 3 = -5
Ejemplo 4 : -3 + 2 = ?
Aquí estamos sumando 2 a menos 3. Comienza con -3 y más 2 veces justo en la recta numérica para llegar a -1.
-3 + 2 = -1
Si un número no tiene signo, generalmente significa que es un número positivo. Por ejemplo, 5 es +5
Suma
Al sumar un positivo a un positivo o un negativo a un negativo, súmalos y dales el mismo signo. Por ejemplo, 5 + 5 es igual a 10, mientras que -5 + -7 es -12.
Al sumar un número positivo y un número negativo, usa la resta tomando el valor absoluto (los números sin sus signos) y resta el menor del mayor. Luego da a la respuesta el signo del número mayor. Por ejemplo, -7 + 4 significa que tomas 7, restas 4 y le das a la respuesta un signo negativo ya que el valor absoluto de -7 es mayor que 4.
Sustracción
Restar un número negativo de algo es lo mismo que sumarle un número positivo. Por ejemplo, restar el número negativo −8 del número 6 es lo mismo que sumar el número 6 y el número 8. En símbolos:
6 − (-8) = 6 + 8 = 14
Al restar un negativo de otro negativo, como -6 y -4, cambie -4 a 4 positivo y sume los valores para tener -6 + 4, dando -2 siguiendo las reglas de suma.
-6 − (-4) = -6 + 4 = -2
Para restar un número positivo y negativo, 12 - (-9), cambia el -9 por 9 y suma los valores para obtener 21.
12 − (-9) = 12 + 9 = 21
Multiplicación
Un número positivo multiplicado por un número negativo te da un número negativo. Por ejemplo, multiplicar el número positivo 3 por el número negativo -2 es lo mismo que multiplicar el número 3 por el número 2 y el resultado tendrá signo negativo.
(3) × (-2) = -6
Un número negativo multiplicado por otro número negativo te da un número positivo. Por ejemplo, multiplicar el número negativo -3 por el número negativo -2 es lo mismo que multiplicar el número 3 por el número 2 pero la respuesta es positiva.
(-3) × (-2) = 6
División
En la división, las reglas varían ligeramente de la multiplicación.
Un número positivo dividido por un positivo siempre es positivo. Por ejemplo, cuando divides el número positivo 15 por el número positivo 3, obtienes 5.
15 ÷ 3 = 5
Un número negativo dividido por un positivo o un número positivo dividido por un negativo siempre será negativo. Por ejemplo, cuando divides el número negativo -15 por el número positivo 3, obtienes -5. Además, cuando divides el número positivo 15 por el número negativo -3, obtienes -5.
15 ÷ (-3) = (-5)
Al dividir un número negativo por otro número negativo, divides el valor absoluto entre sí y obtienes un número positivo. Por ejemplo, cuando divides el número negativo -15 por el número negativo -3, obtienes 5.
(-15) ÷ (-3) = 5