သုညထက်နည်းသော ဂဏန်းကို အနှုတ်နံပါတ်အဖြစ် သိကြပြီး သုညထက်ကြီးသော ဂဏန်းကို အပြုသဘောဆောင်သော ဂဏန်းဟု ခေါ်သည်။ သုညသည် အပြုသဘောမဟုတ်သလို အနုတ်လက္ခဏာလည်း မဟုတ်ပါ။
ကိန်းပြည့်များသည် သုညအပါအဝင် အပေါင်းနှင့် အနုတ်လက္ခဏာ အပေါင်းပါရှိသော အစစ်အမှန် ဂဏန်းများ၏ အခွဲတစ်ခုဖြစ်သည်။ ကိန်းပြည့်များကို {...,-3,-2,-1,0,1,2,3,...} အဖြစ် ကိုယ်စားပြုနိုင်ပြီး ရေတွက်ခြင်း၊ တိုင်းတာခြင်းနှင့် ဖော်ပြခြင်းကဲ့သို့သော သင်္ချာဆိုင်ရာ လုပ်ဆောင်ချက်များနှင့် အပလီကေးရှင်းအမျိုးမျိုးတွင် အသုံးပြုပါသည်။ ပမာဏ။
အနုတ်လက္ခဏာနံပါတ်ကို အနှုတ်လက္ခဏာဖြင့် ရေးပါ။
အနုတ်နံပါတ်များသည် နံပါတ်လိုင်းပေါ်ရှိ သုည၏ ကျန်ရှိသည်။ ဂဏန်းတစ်ခုနှင့် ၎င်း၏ ဆန့်ကျင်ဘက် (သို့မဟုတ် အနုတ်) သည် သုညနှင့် အကွာအဝေး အမြဲတူညီသည်။ အနှုတ်နံပါတ် -2 သည် သုည၏ဘယ်ဘက်တွင် သုည၏ညာဘက်မှ 2 အထိဖြစ်သည်။
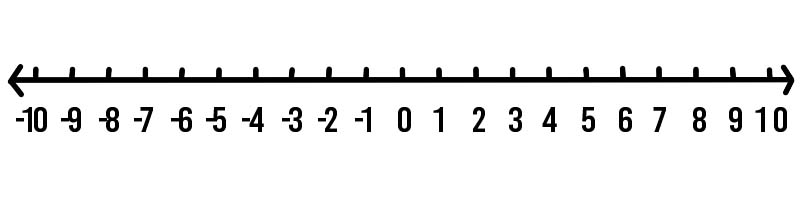
အနုတ်ကိန်းများကို အလွယ်တကူ သတိပြုမိသည့် လက်တွေ့ကမ္ဘာ ဥပမာကို ကြည့်ကြပါစို့။ တစ်စုံတစ်ခုသည် မည်မျှပူသည်ဖြစ်စေ အေးသည်ဖြစ်စေ အပူချိန်ကို တိုင်းတာသည်။ မနက်ဖြန်တွင် ယနေ့ထက် ၄ ဒီဂရီပိုအေးမည်ဟု မိုးလေဝသခန့်မှန်းချက် ခန့်မှန်းသည့် မြင်ကွင်းကို သုံးသပ်ကြည့်ကြပါစို့။ ယနေ့အပူချိန်သည် ၃ ဒီဂရီစင်တီဂရိတ်ဖြစ်သည်။ မနက်ဖြန် အပူချိန် ဘယ်လောက်ရှိမလဲ။ အောက်ပါ နံပါတ်လိုင်းကို အသုံးပြု၍ လေ့လာကြည့်ရအောင်။
မနက်ဖြန်ရဲ့ အပူချိန်က ဘာဖြစ်မယ်ဆိုတာကို သိချင်ရင် 3 မှာစပြီး အဆင့် 4 ကိုပြန်သွားပါ။
ဤတွင် ကျွန်ုပ်တို့သည် အပူချိန် -1 ၏ ရောက်ရှိသည်။ -1 သည် 3 ထက် ပိုအေးသည်ကို သတိပြုပါ။
နံပါတ်လိုင်း၏ ညာဘက်သို့ ရောက်သွားသည်နှင့်အမျှ အပြုသဘောတန်ဖိုး တိုးလာသည်၊ အလားတူ နံပါတ်လိုင်းမှ ဘယ်ဘက်သို့ သွားသည့်အခါ အနုတ်တန်ဖိုး တိုးလာသည်။ သို့သော် -100 သည် -1 ထက်များစွာသေးငယ်သည်ကိုသတိရပါ။ နံပါတ်မျဉ်းပေါ်ရှိ ညာဘက်မှ ပိုဝေးသော ဂဏန်းများသည် ပိုကြီးသည် သို့မဟုတ် ပိုကြီးသည်၊ ဘယ်ဘက်နှင့် ပိုဝေးသော ဂဏန်းများသည် သေးသည် သို့မဟုတ် ပိုနည်းသည်။
အနုတ်လက္ခဏာနံပါတ်များကို သတိပြုမိသည့် အခြားအခြေအနေမှာ ဘဏ်စာရင်းရှင်းတမ်းတွင် ဖြစ်သည်။ ပြီးခဲ့သောလတွင် ကျွန်ုပ်တို့ $300 အပ်နှံပြီး ဘဏ်ရှင်းတမ်းကို လက်ခံရရှိသည့် မြင်ကွင်းတစ်ခုကို သုံးသပ်ကြည့်ကြပါစို့။
ပြီးခဲ့သည့်လ၏ လက်ကျန် = 300
ဓာတ်ဆီဆိုင် = အမှတ်-၂၀
ဌာနဆိုင်ရာစတိုး = -၅၀
စုစုပေါင်းလက်ကျန် = 230
အနုတ်ဂဏန်းများ -20 နှင့် -50 သည် အသုံးစရိတ်များကို ကိုယ်စားပြုပြီး အပြုသဘောဆောင်သော နံပါတ်များသည် အကောင့်သို့ ခရက်ဒစ် သို့မဟုတ် အပ်ငွေကို ကိုယ်စားပြုသည်။
ဥပမာ 1 : 2 − 5 = ?
ဒါကို နံပါတ်တစ်ကြောင်းနဲ့ ဖြေရှင်းကြည့်ရအောင်
2 ၏ဘယ်ဘက်သို့ 5 ကြိမ်ရွှေ့ပါ။
2 - 5 = -3
နုတ်ရန်၊ နောက်သို့ရွှေ့ရန် သို့မဟုတ် ဘယ်ဘက်သို့၊ ဂဏန်းလိုင်းပေါ်ရှိ။
ဥပမာ 2 : -2 + 2 = ?
အနှုတ် 2 ဖြင့် စတင်ပြီး နံပါတ်လိုင်းပေါ်တွင် ညာဘက် 2 ကြိမ်ရွှေ့ပါ။
0 က 0 မို့ -2 + 2 = 0 ။
နံပါတ်လိုင်းပေါ်တွင် ထည့်ရန်၊ ရှေ့သို့ရွှေ့ရန် သို့မဟုတ် ညာဘက်သို့ ရွှေ့ပါ။
ဥပမာ 3 : -2 − 3 = ?
အနှုတ် 2 ဖြင့်စတင်ပြီး နံပါတ်လိုင်းတွင် ဘယ်ဘက် 3 ကြိမ်ရွှေ့ပါ။
-2 − 3 = -5
ဥပမာ 4 : -3 + 2 = ?
ဤတွင် ကျွန်ုပ်တို့သည် 2 ကို အနှုတ် 3 သို့ ပေါင်းထည့်နေပါသည်။ -1 သို့ရောက်ရှိရန် ဂဏန်းလိုင်းပေါ်တွင် -3 နှင့် နောက်ထပ် 2 ကြိမ်စတင်ပါ။
-3 + 2 = -1
နံပါတ်တစ်ခုတွင် လက္ခဏာမပြပါက အများအားဖြင့် ၎င်းသည် အပြုသဘောဆောင်သော ဂဏန်းဖြစ်သည်ဟု ဆိုလိုသည်။ ဥပမာ 5 သည် +5 ဖြစ်သည်။
ထပ်လောင်း
အပြုသဘောမှ အပြုသဘော သို့မဟုတ် အနုတ်အား အနုတ်သဘောသို့ ပေါင်းထည့်သောအခါ ၎င်းတို့ကို ပေါင်းထည့်ကာ တူညီသော လက္ခဏာကို ပေးဆောင်ပါ။ ဥပမာအားဖြင့်၊ 5+5 သည် 10 နှင့် ညီမျှပြီး -5 + -7 သည် -12 ဖြစ်သည်။
အပေါင်းကိန်းများနှင့် အနုတ်ကိန်းများကို ပေါင်းထည့်သောအခါ၊ အကြွင်းမဲ့တန်ဖိုး—လက္ခဏာမရှိသော ဂဏန်းများ—ကိုယူခြင်းဖြင့် နုတ်ကိုသုံးကာ အသေးကို အကြီးမှ နုတ်ပါ။ ပြီးရင် အဖြေကို ပိုကြီးတဲ့ ဂဏန်းရဲ့ လက္ခဏာကို ပေးလိုက်ပါ။ ဥပမာ -7 + 4 ဆိုသည်မှာ သင် 7 ကို နုတ်ပြီး 4 ကို နုတ်ပြီး အဖြေကို -7 ၏ ပကတိတန်ဖိုးသည် 4 ထက် ကြီးသောကြောင့် အဖြေကို အနှုတ်လက္ခဏာ ပေးသည်။
နုတ်ခြင်း။
တစ်ခုခုမှ အနှုတ်ကိန်းတစ်ခုကို နုတ်ခြင်းသည် ၎င်းတွင် အပေါင်းကိန်းထည့်ခြင်းနှင့် အတူတူပင်။ ဥပမာအားဖြင့်၊ နံပါတ် 6 မှ အနုတ် ဂဏန်း −8 ကို နုတ်ရန် သည် နံပါတ် 6 နှင့် နံပါတ် 8 ကို ပေါင်းထည့်ခြင်း နှင့် အတူတူပင်ဖြစ်သည်။
6 − (-8) = 6 + 8 = 14
-6 နှင့် -4 ကဲ့သို့သော အနှုတ်မှ အနှုတ်ကို နုတ်သည့်အခါ -4 မှ အပေါင်း 4 သို့ပြောင်းပြီး -6 + 4 ရှိရန် တန်ဖိုးများကို ပေါင်းထည့်ကာ -2 ကို ထပ်လောင်းစည်းမျဉ်းများအတိုင်း ပေးသည်။
-6 − (-4) = -6 + 4 = -2
အပြုသဘောနှင့် အနှုတ်ဂဏန်းကို နုတ်ရန် 12 - (-9)၊ -9 မှ 9 သို့ပြောင်းပြီး 21 ရရှိရန် တန်ဖိုးများကို ထည့်ပါ။
12 − (-9) = 12 + 9 = 21
ပွား
အနှုတ်ကိန်းဖြင့် မြှောက်ထားသော အပေါင်းကိန်းသည် သင့်အား အနှုတ်နံပါတ်တစ်ခုပေးသည်။ ဥပမာအားဖြင့်၊ အပေါင်းကိန်း 3 ကို အနှုတ်နံပါတ် -2 ဖြင့် မြှောက်ခြင်းသည် 3 ကို နံပါတ် 2 ဖြင့် မြှောက်ခြင်း နှင့် တူညီပြီး ရလဒ်သည် အနှုတ်လက္ခဏာ ပေါ်လာလိမ့်မည်။
(၃) × (-၂) = -၆
အနုတ်နံပါတ်သည် အခြားအနှုတ်နံပါတ်ဖြင့် မြှောက်ထားသော အပေါင်းကိန်းတစ်ခုပေးသည်။ ဥပမာအားဖြင့်၊ အနုတ်နံပါတ်-၃ ကို အနုတ်နံပါတ်-၂ ဖြင့် မြှောက်ခြင်းသည် နံပါတ် ၃ ကို နံပါတ် ၂ ဖြင့် မြှောက်ခြင်းနှင့် တူညီသော်လည်း အဖြေမှာ အပြုသဘောဖြစ်သည်။
(-3) × (-2) = ၆
တပ်ခွဲ
ခွဲခြင်းတွင် စည်းမျဉ်းများသည် မြှောက်ခြင်းမှ အနည်းငယ်ကွဲပြားသည်။
အပြုသဘောဖြင့် ပိုင်းခြားထားသော ကိန်းဂဏန်းသည် အမြဲတမ်း အပြုသဘောဖြစ်သည်။ ဥပမာအားဖြင့် အပေါင်း 15 ကို အပေါင်း 3 ဖြင့် ခွဲသောအခါ 5 ကို ရလိမ့်မည်။
15 ÷ 3 = 5
အနုတ်ကိန်းကို အပြုသဘောဖြင့် ပိုင်းခြားသော သို့မဟုတ် အပြုသဘောဆောင်သော ကိန်းဂဏာန်းဖြင့် ပိုင်းခြားထားသော အနုတ်ကိန်းသည် အမြဲတမ်း အနှုတ်ဖြစ်သည်။ ဥပမာအားဖြင့် အနှုတ်နံပါတ်-၁၅ ကို အပြုသဘော နံပါတ် ၃ ဖြင့် ခွဲသောအခါ၊ သင်သည် -၅ ကိုရလိမ့်မည်။ ထို့အပြင် အပေါင်း 15 ကို အနှုတ် ဂဏန်း-3 ဖြင့် ပိုင်းခြားပါက -5 ကို ရရှိမည်ဖြစ်သည်။
15 ÷ (-3) = (-5)၊
အနှုတ်နံပါတ်ကို အနှုတ်နံပါတ်ဖြင့် ပိုင်းခြားသောအခါ၊ သင်သည် ပကတိတန်ဖိုးကို တစ်ခုနှင့်တစ်ခု ပိုင်းခြားပြီး အပေါင်းကိန်းတစ်ခုရရှိမည်ဖြစ်သည်။ ဥပမာအားဖြင့် အနုတ်နံပါတ်-၁၅ ကို အနှုတ်နံပါတ်-၃ ဖြင့် ပိုင်းခြားသောအခါ၊ သင်သည် ၅ ကိုရလိမ့်မည်။
(-15) ÷ (-3) = 5