Liczba mniejsza od zera jest znana jako liczba ujemna, a liczba większa od zera jest znana jako liczba dodatnia. Zero nie jest ani dodatnie, ani ujemne.
Liczby całkowite to podzbiór liczb rzeczywistych, który składa się ze wszystkich dodatnich i ujemnych liczb całkowitych, w tym zera. Liczby całkowite mogą być reprezentowane jako {...,-3,-2,-1,0,1,2,3,...} i są używane w różnych operacjach matematycznych i zastosowaniach, takich jak liczenie, mierzenie i opisywanie wielkie ilości.
Liczbę ujemną zapisujemy przez wstawienie znaku minus
Liczby ujemne są na lewo od zera na osi liczbowej. Liczba i jej przeciwieństwo (lub ujemne) są zawsze w tej samej odległości od zera. Liczba ujemna -2 jest tak daleko na lewo od zera, jak 2 na prawo od zera.
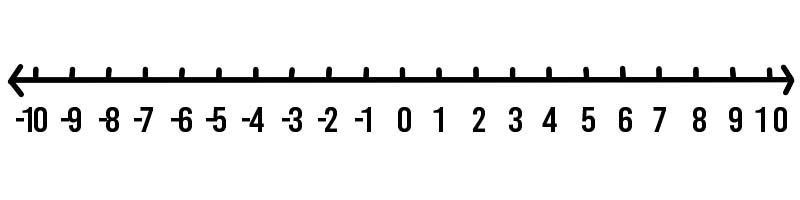
Weźmy rzeczywisty przykład, w którym łatwo zauważyć liczby ujemne. Mierzymy temperaturę, aby wiedzieć, jak coś jest gorące lub zimne. Rozważmy scenariusz, w którym prognoza pogody przewiduje, że jutro będzie o 4 stopnie zimniej niż dzisiaj. Dzisiejsza temperatura to 3 stopnie Celsjusza. Jaka temperatura będzie jutro? Przekonajmy się, korzystając z poniższej linii liczbowej.
Aby dowiedzieć się, jaka będzie jutro temperatura, zacznij od 3 i cofnij się o 4 stopnie.
Tutaj osiągamy temperaturę -1. Zauważ, że -1 jest zimniejsze niż 3.
W miarę przesuwania się w prawo od osi liczbowej rośnie wartość dodatnia, podobnie w miarę przesuwania się w lewo od osi liczbowej rośnie wartość ujemna. Pamiętaj jednak, że -100 jest znacznie mniejsze niż -1. Liczby znajdujące się bardziej na prawo na osi liczbowej są większe lub większe, podczas gdy liczby znajdujące się dalej na lewo są mniejsze lub mniejsze.
Inną sytuacją, w której zauważysz liczby ujemne, jest wyciąg bankowy. Rozważmy scenariusz, w którym w zeszłym miesiącu wpłaciliśmy 300 USD i otrzymaliśmy wyciąg bankowy.
Saldo z ostatniego miesiąca = 300
Stacja benzynowa = -20
Dom towarowy = -50
Całkowite saldo = 230
Liczby ujemne -20 i -50 reprezentują wydatki, a liczby dodatnie oznaczają uznanie lub wpłatę na konto.
Przykład 1 : 2 − 5 = ?
Rozwiążmy to za pomocą osi liczbowej
Przesuń się 5 razy w lewo od 2
2 - 5 = -3
Aby odjąć, przesuń się do tyłu lub w lewo na osi liczbowej.
Przykład 2 : -2 + 2 = ?
Zacznij od minus 2 i przesuń się 2 razy w prawo na osi liczbowej.
Dochodzimy do 0, więc -2 + 2 = 0.
Aby dodać, przejdź do przodu lub w prawo na osi liczbowej.
Przykład 3 : -2 − 3 = ?
Zacznij od minus 2 i przesuń się 3 razy w lewo na osi liczbowej.
-2 − 3 = -5
Przykład 4 : -3 + 2 = ?
Tutaj dodajemy 2 do ujemnej 3. Zacznij od -3 i więcej 2 razy dokładnie na osi liczbowej, aby osiągnąć -1.
-3 + 2 = -1
Jeśli liczba nie ma znaku, zwykle oznacza to, że jest liczbą dodatnią. Na przykład 5 to +5
Dodatek
Dodając pozytyw do pozytywu lub negatyw do negatywu, dodaj je razem i nadaj im ten sam znak. Na przykład 5 + 5 równa się 10, a -5 + -7 równa się -12.
Dodając razem liczbę dodatnią i ujemną, użyj odejmowania, biorąc wartość bezwzględną — liczby bez ich znaków — i odejmij mniejszą od większej. Następnie w odpowiedzi podaj znak większej liczby. Na przykład -7 + 4 oznacza, że bierzesz 7, odejmujesz 4 i dajesz odpowiedzi znak ujemny, ponieważ wartość bezwzględna -7 jest większa niż 4.
Odejmowanie
Odejmowanie od czegoś liczby ujemnej to to samo, co dodawanie do niej liczby dodatniej. Na przykład odjęcie liczby ujemnej −8 od liczby 6 jest równoznaczne z dodaniem liczby 6 i liczby 8. W symbolach:
6 − (-8) = 6 + 8 = 14
Odejmując wartość ujemną od wartości ujemnej, np. -6 i -4, przełącz wartość -4 na wartość dodatnią 4 i dodaj wartości razem, aby uzyskać wartość -6 + 4, co daje -2 zgodnie z zasadami dodawania.
-6 − (-4) = -6 + 4 = -2
Aby odjąć liczbę dodatnią i ujemną, 12 - (-9), zamień -9 na 9 i dodaj wartości, aby uzyskać 21.
12 - (-9) = 12 + 9 = 21
Mnożenie
Liczba dodatnia pomnożona przez liczbę ujemną daje liczbę ujemną. Na przykład pomnożenie liczby dodatniej 3 przez liczbę ujemną -2 jest równoznaczne z pomnożeniem liczby 3 przez liczbę 2, a wynik będzie miał znak ujemny.
(3) × (-2) = -6
Liczba ujemna pomnożona przez inną liczbę ujemną daje liczbę dodatnią. Na przykład pomnożenie liczby ujemnej -3 przez liczbę ujemną -2 jest równoznaczne z pomnożeniem liczby 3 przez liczbę 2, ale odpowiedź jest dodatnia.
(-3) × (-2) = 6
Dział
Zasady dzielenia różnią się nieco od mnożenia.
Liczba dodatnia podzielona przez liczbę dodatnią jest zawsze dodatnia. Na przykład, jeśli podzielisz liczbę dodatnią 15 przez liczbę dodatnią 3, otrzymasz 5.
15 ÷ 3 = 5
Liczba ujemna podzielona przez liczbę dodatnią lub liczba dodatnia podzielona przez liczbę ujemną zawsze będzie ujemna. Na przykład, dzieląc liczbę ujemną -15 przez liczbę dodatnią 3, otrzymasz -5. Ponadto, dzieląc liczbę dodatnią 15 przez liczbę ujemną -3, otrzymasz -5.
15 ÷ (-3) = (-5)
Dzieląc liczbę ujemną przez liczbę ujemną, dzielisz wartość bezwzględną przez siebie i otrzymujesz liczbę dodatnią. Na przykład, dzieląc liczbę ujemną -15 przez liczbę ujemną -3, otrzymasz 5.
(-15) ÷ (-3) = 5