จำนวนที่น้อยกว่าศูนย์เรียกว่าจำนวนลบ และจำนวนที่มากกว่าศูนย์เรียกว่าจำนวนบวก ศูนย์ไม่ใช่ทั้งบวกและลบ
จำนวนเต็มเป็นส่วนย่อยของจำนวนจริงที่ประกอบด้วยจำนวนเต็มบวกและลบทั้งหมดรวมทั้งศูนย์ จำนวนเต็มสามารถแสดงเป็น {...,-3,-2,-1,0,1,2,3,...} และใช้ในการดำเนินการและการประยุกต์ใช้ทางคณิตศาสตร์ที่หลากหลาย เช่น การนับ การวัด และการอธิบาย ปริมาณ
จำนวนลบเขียนโดยการใส่เครื่องหมายลบ
จำนวนลบจะเหลือศูนย์บนเส้นจำนวน จำนวนและค่าตรงข้าม (หรือค่าลบ) จะมีระยะห่างจากศูนย์เท่ากันเสมอ จำนวนลบ -2 อยู่ทางซ้ายของศูนย์พอๆ กับ 2 ทางขวาของศูนย์
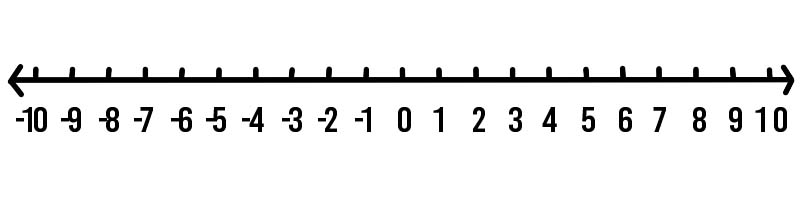
ลองมาเป็นตัวอย่างในโลกแห่งความเป็นจริงที่ตัวเลขติดลบสามารถสังเกตได้ง่าย เราวัดอุณหภูมิเพื่อให้รู้ว่าของร้อนหรือเย็นแค่ไหน ลองพิจารณาสถานการณ์ที่พยากรณ์อากาศคาดการณ์ว่าพรุ่งนี้จะหนาวกว่าวันนี้ 4 องศา อุณหภูมิวันนี้ 3 องศาเซลเซียส พรุ่งนี้อุณหภูมิจะเป็นอย่างไร? ลองหาโดยใช้เส้นจำนวนด้านล่าง
หากต้องการทราบว่าพรุ่งนี้จะมีอุณหภูมิเท่าใด ให้เริ่มที่ 3 และย้อนกลับไป 4 ก้าว
ที่นี่เรามาถึงอุณหภูมิ -1 สังเกตว่า -1 เย็นกว่า 3
เมื่อเราไปทางขวาของเส้นจำนวน ค่าบวกจะเพิ่มขึ้น เช่นเดียวกับที่เราไปทางซ้ายของเส้นจำนวน ค่าลบจะเพิ่มขึ้น แต่จำไว้ว่า -100 นั้นเล็กกว่า -1 มาก ตัวเลขที่ปรากฏอยู่ไกลออกไปทางขวาบนเส้นจำนวนจะมากกว่าหรือมากกว่า ในขณะที่ตัวเลขที่ปรากฏทางด้านซ้ายจะเล็กกว่าหรือน้อยกว่า
อีกสถานการณ์หนึ่งที่คุณสังเกตเห็นตัวเลขติดลบคือในใบแจ้งยอดจากธนาคาร ลองพิจารณาสถานการณ์ที่เราฝากเงิน $300 เมื่อเดือนที่แล้ว และได้รับใบแจ้งยอดจากธนาคาร
ยอดคงเหลือของเดือนที่แล้ว = 300
ปั๊มน้ำมัน = -20
ห้างสรรพสินค้า = -50
ยอดรวม = 230
ตัวเลขที่เป็นลบ -20 และ -50 แสดงถึงค่าใช้จ่าย ในขณะที่ตัวเลขที่เป็นบวกแสดงถึงเครดิตหรือเงินฝากในบัญชี
ตัวอย่างที่ 1 : 2 − 5 = ?
ลองแก้มันด้วยเส้นจำนวนกัน
เลื่อน 5 ครั้งไปทางซ้ายของ 2
2 - 5 = -3
หากต้องการลบ ให้เลื่อนไปข้างหลังหรือไปทางซ้ายบนเส้นจำนวน
ตัวอย่างที่ 2 : -2 + 2 = ?
เริ่มต้นด้วยลบ 2 และเลื่อนไปทางขวา 2 ครั้งบนเส้นจำนวน
เราถึง 0 ดังนั้น -2 + 2 = 0
หากต้องการบวก ให้เลื่อนไปข้างหน้าหรือไปทางขวาบนเส้นจำนวน
ตัวอย่างที่ 3 : -2 − 3 = ?
เริ่มต้นด้วยค่าลบ 2 และเลื่อนไปทางซ้าย 3 ครั้งในเส้นจำนวน
-2 − 3 = -5
ตัวอย่างที่ 4 : -3 + 2 = ?
เรากำลังบวก 2 กับลบ 3 เริ่มด้วย -3 และอีก 2 ครั้งบนเส้นจำนวนจนถึง -1
-3 + 2 = -1
ถ้าตัวเลขไม่มีเครื่องหมาย แสดงว่าเป็นจำนวนบวก ตัวอย่างเช่น 5 คือ +5
ส่วนที่เพิ่มเข้าไป
เมื่อนำบวกไปบวกหรือลบให้บวกกันและให้เครื่องหมายเหมือนกัน ตัวอย่างเช่น 5 + 5 เท่ากับ 10 ในขณะที่ -5 + -7 เท่ากับ -12
เมื่อบวกจำนวนบวกและจำนวนลบเข้าด้วยกัน ให้ใช้การลบโดยใช้ค่าสัมบูรณ์ ซึ่งเป็นตัวเลขที่ไม่มีเครื่องหมาย และลบค่าที่น้อยกว่าออกจากค่าที่มากกว่า จากนั้นให้เครื่องหมายคำตอบของจำนวนที่มากกว่า ตัวอย่างเช่น -7 + 4 หมายความว่าคุณนำ 7 ลบ 4 และให้คำตอบเป็นเครื่องหมายลบ เนื่องจากค่าสัมบูรณ์ของ -7 มากกว่า 4
การลบ
การลบจำนวนลบออกจากบางสิ่งจะเหมือนกับการบวกจำนวนบวกเข้าไป ตัวอย่างเช่น การลบเลขลบ −8 ออกจากเลข 6 จะเหมือนกับการบวกเลข 6 กับเลข 8 ในสัญลักษณ์:
6 − (-8) = 6 + 8 = 14
เมื่อลบค่าลบออกจากค่าลบ เช่น -6 และ -4 ให้เปลี่ยน -4 เป็นค่าบวก 4 แล้วบวกค่าเข้าด้วยกันเพื่อให้ได้ -6 + 4 โดยให้ -2 ตามกฎการบวก
-6 − (-4) = -6 + 4 = -2
หากต้องการลบจำนวนบวกและลบ 12 - (-9) ให้เปลี่ยน -9 เป็น 9 แล้วบวกค่าเพื่อให้ได้ 21
12 − (-9) = 12 + 9 = 21
การคูณ
จำนวนบวกคูณด้วยจำนวนลบจะได้จำนวนลบ ตัวอย่างเช่น การคูณเลขบวก 3 ด้วยเลขลบ -2 จะเหมือนกับการคูณเลข 3 ด้วยเลข 2 และผลลัพธ์ที่ได้จะมีเครื่องหมายลบ
(3) × (-2) = -6
จำนวนลบคูณด้วยจำนวนลบอีกจำนวนหนึ่งจะได้จำนวนบวก ตัวอย่างเช่น การคูณจำนวนลบ -3 ด้วยจำนวนลบ -2 จะเหมือนกับการคูณจำนวน 3 ด้วยจำนวน 2 แต่คำตอบเป็นบวก
(-3) × (-2) = 6
แผนก
ในการหาร กฎแตกต่างจากการคูณเล็กน้อย
จำนวนบวกหารด้วยจำนวนบวกจะเป็นค่าบวกเสมอ ตัวอย่างเช่น เมื่อคุณหารจำนวนบวก 15 ด้วยจำนวนบวก 3 คุณจะได้ 5
15 ÷ 3 = 5
จำนวนลบหารด้วยจำนวนบวกหรือจำนวนบวกหารด้วยค่าลบจะเป็นค่าลบเสมอ ตัวอย่างเช่น เมื่อคุณหารจำนวนลบ -15 ด้วยจำนวนบวก 3 คุณจะได้ -5 นอกจากนี้ เมื่อคุณหารจำนวนบวก 15 ด้วยจำนวนลบ -3 คุณจะได้ -5
15 ÷ (-3) = (-5)
เมื่อหารจำนวนลบด้วยจำนวนลบ คุณจะนำค่าสัมบูรณ์มาหารกันและได้จำนวนบวก ตัวอย่างเช่น เมื่อคุณหารจำนวนลบ -15 ด้วยจำนวนลบ -3 คุณจะได้ 5
(-15) ÷ (-3) = 5