Dairə müstəvi səthə çəkilə bilən 2 ölçülü formadır. Dairə müəyyən bir müstəvidə Mərkəz adlanan sabit bir nöqtədən bərabər məsafədə olan nöqtələrdən ibarətdir.
A, B, C və D dairənin üzərində yerləşən nöqtələrdir. O dairənin mərkəzini təmsil edir. O ilə dairənin hər hansı bir nöqtəsi arasındakı məsafə çevrənin radiusu adlanır.
OA = OB = OD = OC = Çevrənin radiusu
DB = AC = Dairənin diametri
Diametri dairənin radiusundan iki qat böyükdür. Diametr dairənin mərkəzindən keçən və son nöqtələri dairənin üzərində olan hər hansı bir xəttdir. Çevrə dairənin ətrafındakı məsafədir. Biz onu çevrənin perimetri adlandıra bilərik. Diametr dairələri yarımdairə adlanan iki bərabər hissəyə bölür.
Qövs çevrənin bir hissəsi olan əyri xəttdir. AB, BC qövslərdir. Dairənin iki radiusu ilə əhatə olunmuş hissəsinə sektor deyilir. Ən vacib sektor kvadrantdır. Kvadrant dairənin dörddə birini təşkil edir.
Akkord dairənin iki nöqtəsini birləşdirən xətt seqmentidir. AB A və B çevrəsinin iki nöqtəsini birləşdirən akkorddur. Dairənin diametri olan BD çevrənin ən uzun akkordudur. Hər bir akkord dairəni seqment adlanan iki hissəyə bölür. Kiçik seqment kiçik seqment adlanır və böyük seqment böyük seqment adlanır.
Perimetr və Sahə 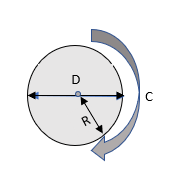
R = Radius, D = Diametr, C = Çevrə
Əgər R radiusdursa, onda dairənin diametri 2 X R-dir.
Bir dairənin perimetri onun çevrəsi adlanır . Çevrə 2 X π XR düsturu ilə hesablana bilər, burada π = 3.14
Dairənin sahəsi A = π XR 2 düsturu ilə hesablana bilər, burada π = 3.14
Mərkəzi bucaq təpəsi dairənin mərkəzi və tərəfləri çevrənin radiusu olan bucaqdır. Tam dairə mərkəzdə 360° bucaq yaradır. Bir dairə qövslər adlanan daha kiçik hissələrə bölünə bilər. Qövslər kiçik qövslərə (mərkəzi bucaq < 180°), böyük qövslərə (mərkəzi bucaq 180° ilə 360° arasındadır) və yarımdairələrə (mərkəzi bucaq = 180°) bölünür.
Sekant bir dairəni düz iki nöqtədə kəsən xəttdir. Tangens xətti dairəni tam olaraq bir nöqtədə kəsir və kəsişmənin baş verdiyi nöqtəyə toxunma nöqtəsi deyilir.