円は、平面に描くことができる 2 次元の形状です。円は、中心と呼ばれる固定点から等距離にある特定の平面上の点で構成されています。
A、B、C、D は円上にある点です。 Oは円の中心を表します。 O と円上の任意の点との間の距離は、円の半径と呼ばれます。
OA = OB = OD = OC = 円の半径
DB = AC = 円の直径
直径は円の半径の 2 倍です。直径は、円の中心を通り、端点が円上にある任意の線です。円周は、円の周りの距離です。これを円周と呼ぶことができます。直径は、円を半円と呼ばれる 2 つの等しい部分に分割します。
円弧は、円周の一部である曲線です。 AB、BCは円弧です。円の 2 つの半径で囲まれた円の一部を扇形と呼びます。最も重要なセクターは象限です。象限は円の 4 分の 1 です。
弦とは、円上の 2 点を結ぶ線分です。 AB は円 A と B 上の 2 点を結ぶ弦です。円の直径である BD は円の最長の弦です。すべてのコードは、円をセグメントと呼ばれる 2 つの部分に分割します。小さい方をマイナーセグメント、大きい方をメジャーセグメントと呼びます。
周囲と面積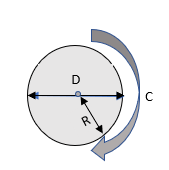
R = 半径、D = 直径、C = 円周
R が半径の場合、円の直径は 2 X R です。
円の周囲を円周といいます。円周は、式 2 X π XR を使用して計算できます。ここで、π = 3.14
円の面積は、式 A = π XR 2 (π = 3.14) を使用して計算できます。
中心角は、頂点が円の中心で、辺が円の半径である角度です。完全な円は、中心で360°の角度になります。円は、円弧と呼ばれる小さな部分に分割できます。円弧は、マイナー アーク (中心角 < 180°)、メジャー アーク (中心角が 180° ~ 360°)、半円 (中心角 = 180°) に分けられます。
セカントは、ちょうど 2 点で円と交差する線です。接線は正確に 1 点で円と交差し、交点が発生する点は接点と呼ばれます。