Тойрог нь хавтгай гадаргуу дээр зурж болох 2 хэмжээст дүрс юм. Тойрог нь төв гэж нэрлэгддэг тогтмол цэгээс ижил зайд байгаа өгөгдсөн хавтгай дээрх цэгүүдээс бүрдэнэ.
A, B, C, D нь тойрог дээр байрлах цэгүүд юм. O тойргийн төвийг илэрхийлнэ. О ба тойрог дээрх дурын цэгийн хоорондох зайг тойргийн радиус гэнэ.
OA = OB = OD = OC = Тойргийн радиус
DB = AC = Тойргийн диаметр
Диаметр нь тойргийн радиусаас хоёр дахин их байна. Диаметр гэдэг нь тойргийн төвийг дайран өнгөрөх, төгсгөлийн цэгүүд нь тойрог дээр байрлах дурын шугам юм. Тойрог нь тойргийг тойрсон зай юм. Бид үүнийг тойргийн периметр гэж нэрлэж болно. Диаметр нь тойргийг хагас тойрог гэж нэрлэгддэг хоёр тэнцүү хэсэгт хуваадаг.
Нуман бол тойргийн нэг хэсэг болох муруй шугам юм. AB, BC нь нумууд юм. Тойргийн хоёр радиусаар хүрээлэгдсэн тойргийн хэсгийг сектор гэнэ. Хамгийн чухал салбар бол квадрант юм. Квадрант нь тойргийн дөрөвний нэг юм.
Хөвч нь тойрог дээрх хоёр цэгийг холбосон шугамын хэсэг юм. AB нь А ба В тойргийн хоёр цэгийг холбодог хөвч юм. Тойргийн диаметр нь BD нь тойргийн хамгийн урт хөвч юм. Хөвч бүр тойргийг сегмент гэж нэрлэдэг хоёр хэсэгт хуваадаг. Жижиг хэсгийг жижиг хэсэг, том хэсгийг том сегмент гэж нэрлэдэг.
Периметр ба талбай 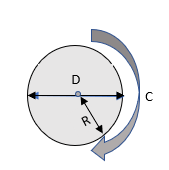
R = Радиус, D = Диаметр, C = Тойрог
Хэрэв R нь радиус бол тойргийн диаметр нь 2 X R байна.
Тойргийн периметрийг түүний тойрог гэнэ. Тойрог 2 X π XR томъёог ашиглан тооцоолж болно, энд π = 3.14
Тойргийн талбайг A = π XR 2 томъёогоор тооцоолж болно, энд π = 3.14
Төв өнцөг нь орой нь тойргийн төв, талууд нь тойргийн радиус болох өнцөг юм. Бүтэн тойрог нь төвд 360 ° өнцөг үүсгэдэг. Тойргийг нум гэж нэрлэдэг жижиг хэсгүүдэд хувааж болно. Нуманууд нь бага нум (төв өнцөг < 180 °), том нумууд (төв өнцөг 180 ° -аас 360 ° хооронд байна) болон хагас тойрог (төв өнцөг = 180 °) гэж хуваагддаг.
Секант гэдэг нь тойргийг яг хоёр цэгээр огтолж буй шугам юм. Шүргэдэг шугам нь тойргийг яг нэг цэгээр огтолдог бөгөөд огтлолцох цэгийг шүргэлтийн цэг гэнэ.