စက်ဝိုင်းသည် လေယာဉ်မျက်နှာပြင်ပေါ်တွင် ရေးဆွဲနိုင်သော 2 Dimensional ပုံသဏ္ဍာန်ဖြစ်သည်။ စက်ဝိုင်းသည် Centre ဟုခေါ်သော ပုံသေအမှတ်မှ ညီမျှသောအကွာအဝေးတွင်ရှိသော အမှတ်များဖြင့် ဖွဲ့စည်းထားသည်။
A, B, C နှင့် D တို့သည် စက်ဝိုင်းပေါ်တွင် တည်ရှိနေသော အမှတ်များဖြစ်သည်။ O စက်ဝိုင်း၏ဗဟိုကိုကိုယ်စားပြုသည်။ O နှင့် စက်ဝိုင်းရှိ မည်သည့်အမှတ်ကြားအကွာအဝေးကို စက်ဝိုင်း၏ အချင်းဝက် ဟုခေါ်သည်။
OA = OB = OD = OC = စက်ဝိုင်း၏ အချင်းဝက်
DB = AC = စက်ဝိုင်း၏ အချင်း
အချင်း သည် စက်ဝိုင်း၏ အချင်းဝက်၏ နှစ်ဆဖြစ်သည်။ Diameter သည် စက်ဝိုင်း၏ အလယ်ဗဟိုကို ဖြတ်သွားသော မျဉ်းကြောင်းဖြစ်ပြီး အဆုံးမှတ်များသည် စက်ဝိုင်းပေါ်တွင် တည်ရှိသည်။ လုံးပတ် သည် စက်ဝိုင်းပတ်ပတ်လည် အကွာအဝေးဖြစ်သည်။ အဲဒါကို စက်ဝိုင်းရဲ့ ပတ်ပတ်လည်လို့ ခေါ်နိုင်တယ်။ အချင်းတစ်ခုသည် စက်ဝိုင်းများကို စက်ဝိုင်းခြမ်းဟုခေါ်သော အညီအမျှ နှစ်ပိုင်းခွဲသည်။
Arc သည် လုံးပတ်၏ အစိတ်အပိုင်းဖြစ်သော မျဉ်းကွေးမျဉ်းဖြစ်သည်။ AB၊ BC တို့သည် arcs ဖြစ်သည်။ စက်ဝိုင်းတစ်ခု၏ အချင်းနှစ်ခုဖြင့် ပတ်ထားသော စက်ဝိုင်း၏ အစိတ်အပိုင်းကို ကဏ္ဍတစ်ခုဟုခေါ်သည်။ အရေးကြီးဆုံးကဏ္ဍသည် လေးထောင့်ကွက်ဖြစ်သည်။ လေးပုံတစ်ပုံသည် စက်ဝိုင်းတစ်ခု၏ လေးပုံတစ်ပုံဖြစ်သည်။
chord သည် စက်ဝိုင်းပေါ်ရှိ အမှတ်နှစ်ခုနှင့် ချိတ်ဆက်ထားသော မျဉ်းအပိုင်းတစ်ခုဖြစ်သည်။ AB သည် စက်ဝိုင်း A နှင့် B တွင် အမှတ်နှစ်ခု ချိတ်ဆက်ထားသော chord တစ်ခုဖြစ်သည်။ စက်ဝိုင်း၏ အချင်းဖြစ်သည့် BD သည် စက်ဝိုင်း၏အရှည်ဆုံး chord ဖြစ်သည်။ chord တစ်ခုစီသည် စက်ဝိုင်းကို segments ဟုခေါ်သော နှစ်ပိုင်းခွဲသည်။ အသေးကို minor segment ဟုခေါ်ပြီး ပိုကြီးသောအပိုင်းကို major segment ဟုခေါ်သည်။
နယ်နိမိတ်နှင့် ဧရိယာ 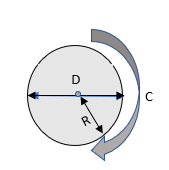
R = Radius, D = Diameter, C = အဝန်း
R သည် အချင်းဝက်ဖြစ်ပါက စက်ဝိုင်း၏ အချင်းသည် 2 X R ဖြစ်သည်။
စက်ဝိုင်းတစ်ခု၏ ပတ်ပတ်လည်ကို ၎င်း၏အဝန်းဟုခေါ်သည် ။ လုံးပတ်ကို ဖော်မြူလာ 2 X π XR ဖြင့် တွက်ချက်နိုင်ပြီး π = 3.14 ဖြစ်သည်။
စက်ဝိုင်းတစ်ခု၏ ဧရိယာအား ဖော်မြူလာ A = π XR 2 ဖြင့် တွက်ချက်နိုင်ပြီး π = 3.14 ၊
ဗဟိုထောင့် သည် စက်ဝိုင်း၏ဗဟိုချက်ဖြစ်ပြီး အစွန်းနှစ်ဖက်သည် စက်ဝိုင်း၏အချင်းဝက်ဖြစ်သည်။ စက်ဝိုင်းအပြည့်သည် အလယ်ဗဟိုတွင် 360° ထောင့်ကို ပြုလုပ်သည်။ စက်ဝိုင်းကို arcs ဟုခေါ်သော အပိုင်းငယ်များအဖြစ် ပိုင်းခြားနိုင်သည်။ Arcs ကို အငယ်စား arcs (ဗဟိုထောင့် < 180°), အဓိက arcs (ဗဟိုထောင့်သည် 180° နှင့် 360° ကြား) နှင့် semicircles (ဗဟိုထောင့် = 180°) ဟူ၍ ပိုင်းခြားထားသည်။
စက္ကန့် တစ်ခုသည် အမှတ်နှစ်ခုတိတိဖြင့် စက်ဝိုင်းတစ်ခုကို ဖြတ်သည့်မျဉ်းတစ်ခုဖြစ်သည်။ တန်းဂျင့် မျဉ်းသည် အမှတ်တစ်ခုတွင် စက်ဝိုင်းတစ်ခုကို ဖြတ်တောက်ပြီး လမ်းဆုံဖြစ်ပေါ်သည့်အမှတ်ကို တင်းနစ်အမှတ်ဟု ခေါ်သည်။