Okrąg to dwuwymiarowy kształt, który można narysować na płaskiej powierzchni. Okrąg składa się z punktów na danej płaszczyźnie, które znajdują się w równej odległości od stałego punktu zwanego środkiem.
A, B, C i D to punkty leżące na okręgu. O reprezentują środek okręgu. Odległość między O a dowolnym punktem na okręgu nazywana jest promieniem okręgu.
OA = OB = OD = OC = Promień okręgu
DB = AC = Średnica koła
Średnica jest dwa razy większa od promienia koła. Średnica to dowolna linia przechodząca przez środek okręgu i której końce leżą na okręgu. Obwód to odległość wokół koła. Możemy to nazwać obwodem koła. Średnica dzieli koła na dwie równe części zwane półkolami.
Łuk to zakrzywiona linia, która jest częścią obwodu. AB, BC to łuki. Część koła ograniczona dwoma promieniami koła nazywana jest sektorem. Najważniejszym sektorem jest kwadrant. Kwadrant to jedna czwarta koła.
Cięciwa to odcinek linii łączący dwa punkty na okręgu. AB to cięciwa łącząca dwa punkty na okręgu A i B. BD, czyli średnica koła, jest najdłuższą cięciwą okręgu. Każdy akord dzieli okrąg na dwie części zwane segmentami . Mniejszy nazywa się segmentem mniejszym, a większy segmentem głównym.
Obwód i powierzchnia 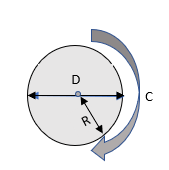
R = promień, D = średnica, C = obwód
Jeśli R jest promieniem, to średnica koła wynosi 2 X R.
Obwód koła nazywamy jego obwodem . Obwód można obliczyć za pomocą wzoru 2 X π XR, gdzie π = 3,14
Pole koła można obliczyć ze wzoru A = π XR 2 gdzie π = 3,14
Kąt środkowy to kąt, którego wierzchołkiem jest środek okręgu, a boki są promieniami okręgu. Pełen okrąg tworzy w środku kąt 360° . Okrąg można podzielić na mniejsze części zwane łukami. Łuki dzielą się na łuki mniejsze (kąt środkowy < 180°), łuki większe (kąt środkowy wynosi od 180° do 360°) i półkola (kąt środkowy = 180°).
Sieczna to prosta przecinająca okrąg dokładnie w dwóch punktach. Linia styczna przecina okrąg dokładnie w jednym punkcie, a punkt, w którym następuje przecięcie, nazywany jest punktem styczności.