Круг - это двумерная форма, которую можно нарисовать на плоской поверхности. Круг состоит из точек на заданной плоскости, которые находятся на равном расстоянии от фиксированной точки, называемой центром.
A, B, C и D - точки, лежащие на окружности. O представляют центр круга. Расстояние между точкой O и любой точкой на окружности называется радиусом окружности.
OA = OB = OD = OC = радиус окружности
DB = AC = Диаметр круга
Диаметр в два раза больше радиуса круга. Диаметр - это любая линия, проходящая через центр окружности и концы которой лежат на окружности. Окружность - это расстояние по окружности. Мы можем назвать это периметром круга. Диаметр делит круги на две равные части, называемые полукругом.
Дуга - это изогнутая линия, которая является частью окружности. AB, BC - дуги. Часть окружности, заключенная в два радиуса окружности, называется сектором. Самый важный сектор - это квадрант. Квадрант - это четверть круга.
Хорда - это отрезок прямой, соединяющий две точки на окружности. AB - это хорда, соединяющая две точки на окружности A и B. BD, который представляет собой диаметр окружности, является самой длинной хордой окружности. Каждый аккорд делит круг на две части, называемые сегментами . Меньший называется второстепенным сегментом, а больший - главным.
Периметр и Площадь 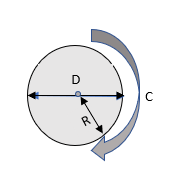
R = радиус, D = диаметр, C = окружность
Если R - радиус, то диаметр окружности равен 2 X R.
Периметр круга называется его окружностью . Окружность можно рассчитать по формуле 2 X π XR, где π = 3,14
Площадь круга можно рассчитать по формуле A = π XR 2, где π = 3,14.
Центральный угол - это угол, вершиной которого является центр окружности, а сторонами - радиусы окружности. Полный круг образует в центре угол 360 °. Круг можно разделить на более мелкие части, называемые дугами. Дуги делятся на малые дуги (центральный угол <180 °), большие дуги (центральный угол от 180 ° до 360 °) и полукруги (центральный угол = 180 °).
Секущая - это линия, пересекающая окружность ровно в двух точках. Касательная линия пересекает окружность ровно в одной точке, а точка пересечения называется точкой касания.