الدوال المثلثية الستة هي: sin، cos، tan، cosec، sec، cot.
دعونا نحاول إيجاد \(\angle A\) في المثلث المعطى.
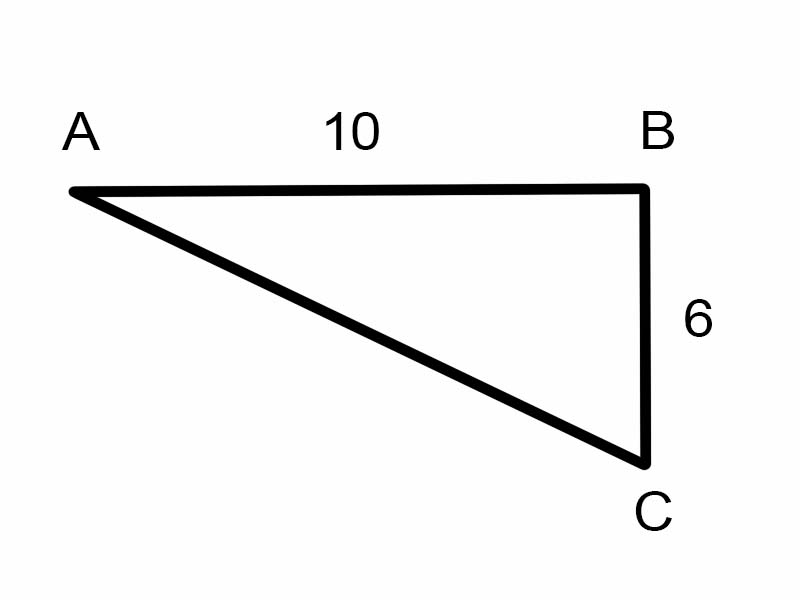
\(\tan A = \frac{6}{10}\)
ولكن هذا لا يساعد في إيجاد قياس \(\angle A\)
نحن بحاجة إلى إيجاد أداة رياضية جديدة لحل مثل هذه المشكلات. دوال الجيب وجيب التمام والظل تأخذ الزوايا وتعطي نسب الأضلاع. ولكننا بحاجة إلى دوال تأخذ نسب الأضلاع وتعطي الزوايا، وبالتالي يتم تقديم الدوال المثلثية العكسية .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
أ = 30.96 درجة [قم بالتقييم باستخدام الآلة الحاسبة]
إذا كان طول ضلعين معروفًا، فيمكن تحديد قياسات الزاوية باستخدام الدالة المثلثية العكسية.
\(\sin^{-1}x \textrm{ أو } \arcsin x\) هي دالة جيبية عكسية.
\(\cos^{-1}x \textrm{ أو } \arccos x \) هي دالة عكسية لـ cos.
\(\tan^{-1}x \textrm{ أو } \arctan x\) هي دالة عكسية للظل.
\(\csc^{-1}x \) أو arccsc x هي دالة csc عكسية.
\(\sec^{-1}x \) أو arcsec x هي دالة sec العكسية.
\(cot^{-1}x \) أو arccot x هي دالة cot العكسية.
في المثلث دع \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [كما \(\sin\theta = \) عمودي ∕ وتر]
يمكننا أن نكتب على النحو التالي \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
يمكننا استنتاج قيمة النسب المثلثية عندما يتم إعطاء \(\theta\) على شكل معكوس وفقًا للجدول أدناه :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
المثال 1: يستند سلم على الحائط، فيصنع زاوية θ مع الأرض. قاعدة السلم تبعد 3 أمتار عن الحائط، ويبلغ طول السلم 5 أمتار. أوجد θ.
حل:
بما أن لدينا الوتر (5 م) والضلع المجاور (3 م)، نستخدم دالة جيب التمام:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) استخدم الآلة الحاسبة لاستنتاج قيمة θ، \(\theta \approx 53.13^{\circ}\)
المثال 2: قم بتقييم \(cos^{−1}(\frac{-1}{2}) \)
حل:
باستخدام خاصية الانعكاس: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
استبدال \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
المثال 3: أوجد \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
حل:
باستخدام المتطابقة: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
في الدوال المثلثية العكسية ، يشير المجال إلى مجموعة قيم الإدخال (قيم x) التي يتم تعريف الدالة لها، ويشير النطاق إلى مجموعة قيم الإخراج (قيم y) التي يمكن أن تأخذها الدالة.
فيما يلي مجالات ونطاقات الدوال المثلثية العكسية الست:
| نطاق | مجال | الوظيفة |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |