Altı triqonometrik funksiyalar sin, cos, tan, cosec, sec və cot-dur.
Verilmiş üçbucaqda \(\angle A\) tapmağa çalışaq.
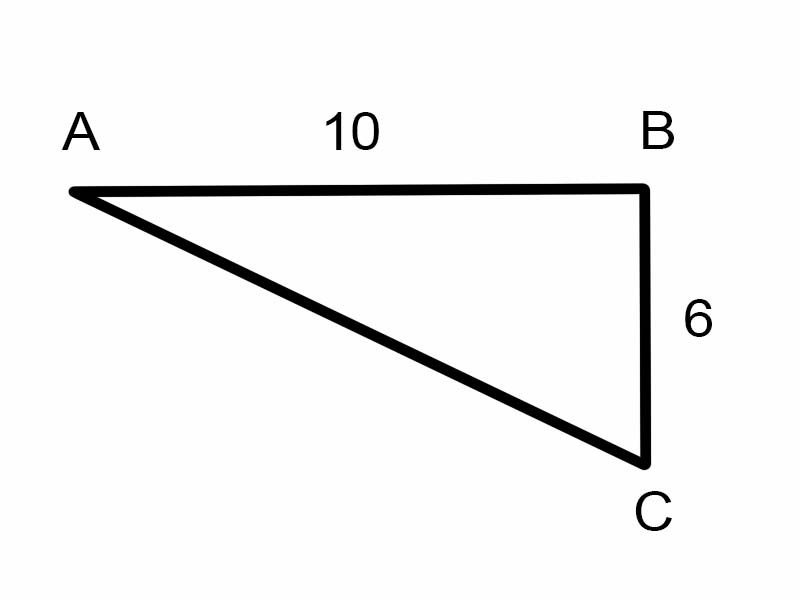
\(\tan A = \frac{6}{10}\)
Lakin bu \(\angle A\) ölçüsünü tapmaq üçün faydalı deyil.
Bu kimi problemləri həll etmək üçün yeni riyazi alət tapmalıyıq. Sinus, Kosinus və Tangens funksiyaları bucaq alır və yan nisbətlər verir. Ancaq bizə yan nisbətləri götürən və bucaq verən funksiyalar lazımdır və buna görə də Tərs Triqonometrik funksiyalar təqdim olunur.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Kalkulyatorla qiymətləndirin]
İki tərəfin uzunluğu məlumdursa, tərs triqonometrik funksiyadan istifadə edərək bucaq ölçüləri təyin edilə bilər.
\(\sin^{-1}x \textrm{ və ya } \arcsin x\) tərs sinus funksiyasıdır.
\(\cos^{-1}x \textrm{ və ya } \arccos x \) tərs cos funksiyasıdır.
\(\tan^{-1}x \textrm{ və ya } \arctan x\) tərs tan funksiyasıdır.
\(\csc^{-1}x \) və ya arccsc x tərs csc funksiyasıdır.
\(\sec^{-1}x \) və ya arcsec x tərs saniyə funksiyasıdır.
\(cot^{-1}x \) və ya arccot x tərs çarpayı funksiyasıdır.
Üçbucaqda qoy \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [ \(\sin\theta = \) Perpendikulyar∕ Hipotenuz kimi]
\({x \over 1} = \frac{AB}{AC}\) kimi yaza bilərik
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Aşağıdakı cədvələ uyğun olaraq \(\theta\) tərs verildikdə triqonometrik nisbətlərin qiymətini əldə edə bilərik :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Nümunə 1: Nərdivan divara söykənərək yerlə θ bucağı yaradır. Pilləkənin əsası divardan 3 metr aralıda, nərdivanının uzunluğu isə 5 metrdir. θ tapın.
Həlli:
Hipotenuza (5 m) və ona bitişik tərəfə (3 m) sahib olduğumuz üçün kosinus funksiyasından istifadə edirik:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) θ dəyərini əldə etmək üçün kalkulyatordan istifadə edin, \(\theta \approx 53.13^{\circ}\)
Nümunə 2: Qiymətləndirin \(cos^{−1}(\frac{-1}{2}) \)
Həlli:
Yansıtma xüsusiyyətindən istifadə edərək: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\( x=\frac{1}{2} \) ilə əvəz olunur
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Misal 3: Qiymətləndirin \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Həlli:
Şəxsiyyətdən istifadə: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Tərs triqonometrik funksiyalarda sahə funksiyanın təyin olunduğu giriş dəyərləri (x-dəyərləri) çoxluğuna, diapazon isə funksiyanın qəbul edə biləcəyi çıxış dəyərlərinin (y-dəyərləri) çoxluğuna aiddir.
Altı tərs triqonometrik funksiyanın domenləri və diapazonları bunlardır:
| Funksiya | Domen | diapazonu |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |