ছয়টি ত্রিকোণমিতিক ফাংশন হল sin, cos, tan, cosec, sec এবং cot।
আসুন আমরা প্রদত্ত ত্রিভুজে \(\angle A\) খুঁজে বের করার চেষ্টা করি।
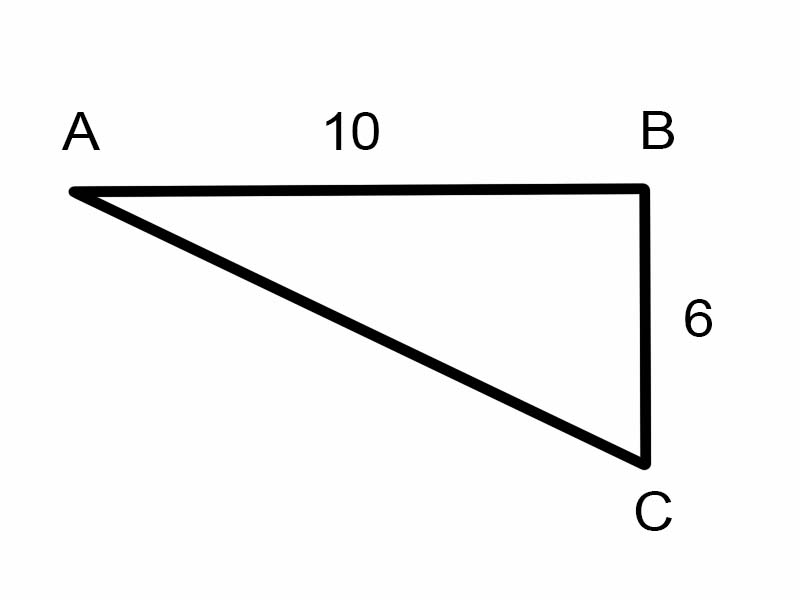
\(\tan A = \frac{6}{10}\)
কিন্তু \(\angle A\) এর পরিমাপ বের করার জন্য এটি সহায়ক নয়।
এই ধরণের সমস্যা সমাধানের জন্য আমাদের একটি নতুন গাণিতিক হাতিয়ার খুঁজে বের করতে হবে। সাইন, কোসাইন এবং ট্যানজেন্ট ফাংশন কোণ নেয় এবং পার্শ্ব অনুপাত দেয়। কিন্তু আমাদের এমন ফাংশন প্রয়োজন যা পার্শ্ব অনুপাত নেয় এবং কোণ দেয় এবং তাই বিপরীত ত্রিকোণমিতিক ফাংশন চালু করা হয়।
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [ক্যালকুলেটর দিয়ে মূল্যায়ন করুন]
যদি দুটি বাহুর দৈর্ঘ্য জানা থাকে, তাহলে বিপরীত ত্রিকোণমিতিক ফাংশন ব্যবহার করে কোণ পরিমাপ নির্ধারণ করা যেতে পারে।
\(\sin^{-1}x \textrm{ অথবা } \arcsin x\) হল বিপরীত সাইন ফাংশন।
\(\cos^{-1}x \textrm{ অথবা } \arccos x \) হল বিপরীত cos ফাংশন।
\(\tan^{-1}x \textrm{ অথবা } \arctan x\) হল বিপরীত tan ফাংশন।
\(\csc^{-1}x \) অথবা arccsc x হল বিপরীত csc ফাংশন।
\(\sec^{-1}x \) অথবা arcsec x হল বিপরীত sec ফাংশন।
\(cot^{-1}x \) অথবা arccot x হল বিপরীত cot ফাংশন।
একটি ত্রিভুজে ধরুন \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [যেমন \(\sin\theta = \) লম্ব∕ কর্ণ]
আমরা লিখতে পারি \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
নিচের সারণি অনুসারে \(\theta\) বিপরীতভাবে দেওয়া হলে আমরা ত্রিকোণমিতিক অনুপাতের মান বের করতে পারি :
১. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
২. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
৩. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
উদাহরণ ১: একটি মই একটি দেয়ালের সাথে হেলে আছে, মাটির সাথে θ কোণ তৈরি করে। মইয়ের ভিত্তি দেয়াল থেকে 3 মিটার দূরে এবং মইটি 5 মিটার লম্বা। θ নির্ণয় করো।
সমাধান:
যেহেতু আমাদের কর্ণ (5 মি) এবং সংলগ্ন বাহু (3 মি), আমরা কোসাইন ফাংশন ব্যবহার করি:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) θ এর মান বের করতে ক্যালকুলেটর ব্যবহার করুন, \(\theta \approx 53.13^{\circ}\)
উদাহরণ ২: \(cos^{−1}(\frac{-1}{2}) \) মূল্যায়ন করুন
সমাধান:
প্রতিফলন বৈশিষ্ট্য ব্যবহার করে: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
প্রতিস্থাপন করা হচ্ছে \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
উদাহরণ ৩: \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \) মূল্যায়ন করুন
সমাধান:
পরিচয় ব্যবহার করে: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
বিপরীত ত্রিকোণমিতিক ফাংশনে , ডোমেন বলতে ইনপুট মানের সেট (x-মান) বোঝায় যার জন্য ফাংশনটি সংজ্ঞায়িত করা হয়, এবং পরিসর বলতে ফাংশনটি যে আউটপুট মানের সেট (y-মান) নিতে পারে তা বোঝায়।
ছয়টি বিপরীত ত্রিকোণমিতিক ফাংশনের ডোমেন এবং পরিসর এখানে দেওয়া হল:
| ফাংশন | ডোমেন | রেঞ্জ |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |