Back to the topics list

inverse trigonometrische funktionen

Die sechs trigonometrischen Funktionen sind sin, cos, tan, cosec, sec und cot.

Versuchen wir \(\angle A\) im gegebenen Dreieck zu finden.

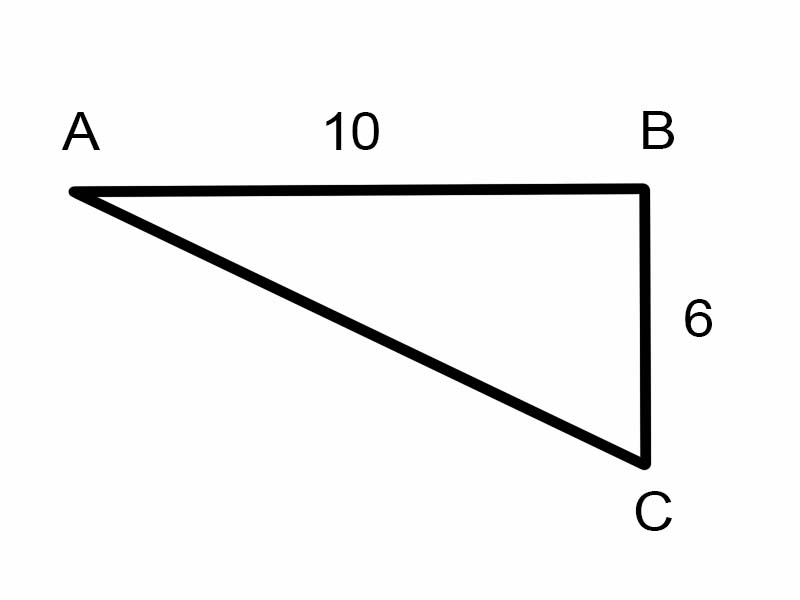
\(\tan A = \frac{6}{10}\)

Dies ist jedoch nicht hilfreich, um das Maß von \(\angle A\) zu finden.

Wir müssen ein neues mathematisches Werkzeug finden, um Probleme wie diese zu lösen. Die Funktionen Sinus, Cosinus und Tangens berechnen Winkel und geben Seitenverhältnisse an. Aber wir brauchen Funktionen, die Seitenverhältnisse berechnen und Winkel angeben, und deshalb werden inverse trigonometrische Funktionen eingeführt.

\(\tan A = \frac{6}{10}\)

\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)

A = 30,96° [Mit dem Rechner auswerten]

Wenn die Länge zweier Seiten bekannt ist, können Winkelmaße mithilfe der inversen trigonometrischen Funktion bestimmt werden.

\(\sin^{-1}x \textrm{ oder } \arcsin x\) ist die inverse Sinusfunktion.

\(\cos^{-1}x \textrm{ oder } \arccos x \) ist die inverse Cosinusfunktion.

\(\tan^{-1}x \textrm{ oder } \arctan x\) ist die inverse Tan-Funktion.

\(\csc^{-1}x \) oder arccsc x ist die inverse csc-Funktion.

\(\sec^{-1}x \) oder Bogensekunden x ist die inverse Sekundenfunktion.

\(cot^{-1}x \) oder arccot x ist die inverse Cot-Funktion.

Beziehung zwischen Trigonometrie und inversen Trigonometriefunktionen

In einem Dreieck sei \(\sin \theta = x\)

⇒ \(\sin \theta = {x \over 1}\) [als \(\sin\theta = \) Senkrechte∕ Hypothenuse]

Wir können schreiben als \({x \over 1} = \frac{AB}{AC}\)

\(AC^2 = AB^2 + BC^2\)

⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)

Wir können den Wert trigonometrischer Verhältnisse ableiten, wenn \(\theta\) gemäß der folgenden Tabelle als Inverse angegeben wird :
1. \(\theta = \sin^{-1}x\)

2. \(\theta = \cos^{-1}x\)

3. \(\theta = \tan^{-1}x\)

Können Sie jetzt die Werte von \(\csc^{-1} x\) , \(\sec^{-1}x\) , \(\cot^{-1}x\) ableiten?

Beziehung zwischen inversen trigonometrischen Funktionen:

\(\sin^{-1}(-x) = - \sin^{-1} x\)

\(\tan^{-1}(-x) = - \tan^{-1} x\)

\(\csc^{-1}(-x) = - \csc^{-1} x\)

\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)

\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)

\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)

\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)

\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)

\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)

\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)

\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)

\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)

\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)

Beispiele:

Beispiel 1: Eine Leiter lehnt an einer Wand und bildet mit dem Boden einen Winkel θ. Die Basis der Leiter ist 3 Meter von der Wand entfernt und die Leiter ist 5 Meter lang. Berechnen Sie θ.

Lösung:
Da wir die Hypothenuse (5 m) und die Ankathete (3 m) haben, verwenden wir die Cosinusfunktion:

\(\cos \theta = {3 \over 5}\)

\(\theta = \cos^{-1} ({3 \over 5})\) Berechnen Sie mit dem Rechner den Wert von θ, \(\theta \approx 53.13^{\circ}\)

Beispiel 2: Berechnen Sie \(cos⁡^{−1}(\frac{-1}{2}) \)

Lösung:

Verwenden der Reflexionseigenschaft: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)

Ersetzen von \( x=\frac{1}{2} \)

\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)

Beispiel 3: Berechnen Sie \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)

Lösung:

Unter Verwendung der Identität: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)

\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)

Definitions- und Wertebereich inverser trigonometrischer Funktionen

Bei inversen trigonometrischen Funktionen bezieht sich die Definitionsmenge auf die Menge der Eingabewerte (x-Werte), für die die Funktion definiert ist, und der Wertebereich auf die Menge der Ausgabewerte (y-Werte), die die Funktion annehmen kann.

Hier sind die Definitions- und Wertebereiche der sechs inversen trigonometrischen Funktionen: