The six trigonometric functions are sin, cos, tan, cosec, sec and cot.
Let us try to find \(\angle A\) in the given triangle.
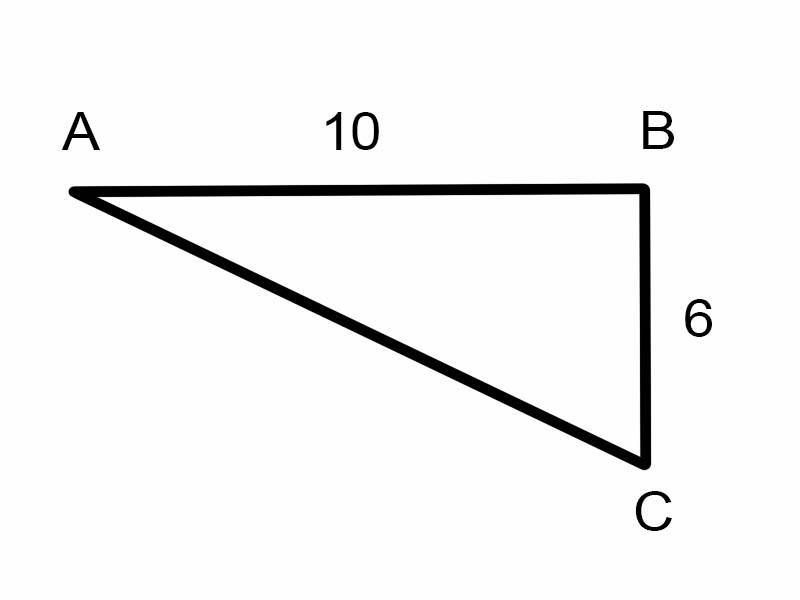
\(\tan A = \frac{6}{10}\)
But this is not helpful to find the measure of \(\angle A\)
We need to find a new mathematical tool to solve problems like these. Sine, Cosine and Tangent functions take angles and give side ratios. But we need functions that take side ratios and give angles and therefore Inverse Trigonometric functions are introduced.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [Evaluate with the calculator]
If the length of two sides are known, angle measures can be determined using the inverse trigonometric function.
\(\sin^{-1}x \textrm{ or } \arcsin x\) is inverse sine function.
\(\cos^{-1}x \textrm{ or } \arccos x \) is inverse cos function.
\(\tan^{-1}x \textrm{ or } \arctan x\) is inverse tan function.
\(\csc^{-1}x \) or arccsc x is inverse csc function.
\(\sec^{-1}x \) or arcsec x is inverse sec function.
\(cot^{-1}x \) or arccot x is inverse cot function.
In a triangle let \(\sin \theta = x\)
⇒\(\sin \theta = {x \over 1}\) [as \(\sin\theta = \) Perpendicular∕ Hypotenuse]
We can write as \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
We can derive value of trigonometric ratios when \(\theta\) is given as inverse according to below table:
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Example 1: A ladder leans against a wall, making an angle θ with the ground. The base of the ladder is 3 meters away from the wall, and the ladder is 5 meters long. Find θ.
Solution:
Since we have the hypotenuse (5 m) and the adjacent side (3 m), we use the cosine function:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Use calculator to derive the value of θ, \(\theta \approx 53.13^{\circ}\)
Example 2: Evaluate \(cos^{−1}(\frac{-1}{2}) \)
Solution:
Using the reflection property: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Substituting \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Example 3: Evaluate \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Solution:
Using the identity: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
In inverse trigonometric functions, the domain refers to the set of input values (x-values) for which the function is defined, and the range refers to the set of output values (y-values) that the function can take.
Here are the domains and ranges of the six inverse trigonometric functions:
| Function | Domain | Range |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\), \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) |
\(0 \le y \le {\pi}\), \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |