Las seis funciones trigonométricas son sin, cos, tan, cosec, sec y cot.
Intentemos encontrar \(\angle A\) en el triángulo dado.
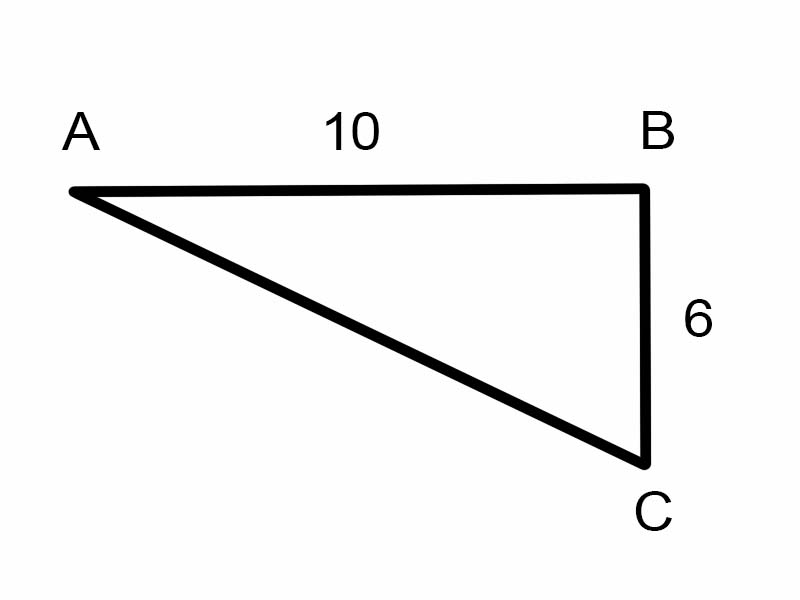
\(\tan A = \frac{6}{10}\)
Pero esto no es útil para encontrar la medida del \(\angle A\)
Necesitamos encontrar una nueva herramienta matemática para resolver problemas como estos. Las funciones seno, coseno y tangente toman ángulos y dan razones entre los lados. Pero necesitamos funciones que tomen razones entre los lados y den ángulos y, por lo tanto, se introducen las funciones trigonométricas inversas .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Evaluar con la calculadora]
Si se conoce la longitud de dos lados, las medidas de los ángulos se pueden determinar utilizando la función trigonométrica inversa.
\(\sin^{-1}x \textrm{ o } \arcsin x\) es la función seno inversa.
\(\cos^{-1}x \textrm{ o } \arccos x \) es la función cos inversa.
\(\tan^{-1}x \textrm{ o } \arctan x\) es la función tan inversa.
\(\csc^{-1}x \) o arccsc x es la función csc inversa.
\(\sec^{-1}x \) o arcsec x es la función sec inversa.
\(cot^{-1}x \) o arccot x es la función cot inversa.
En un triángulo sea \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [como \(\sin\theta = \) Perpendicular ∕ Hipotenusa]
Podemos escribir como \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Podemos derivar el valor de las razones trigonométricas cuando \(\theta\) se da como inversa de acuerdo con la siguiente tabla :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Ejemplo 1: Una escalera se apoya contra una pared y forma un ángulo θ con el suelo. La base de la escalera está a 3 metros de la pared y la escalera tiene 5 metros de largo. Halla θ.
Solución:
Como tenemos la hipotenusa (5 m) y el lado adyacente (3 m), utilizamos la función coseno:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Utilice la calculadora para derivar el valor de θ, \(\theta \approx 53.13^{\circ}\)
Ejemplo 2: Evaluar \(cos^{−1}(\frac{-1}{2}) \)
Solución:
Usando la propiedad de reflexión: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Sustituyendo \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Ejemplo 3: Evaluar \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Solución:
Usando la identidad: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
En funciones trigonométricas inversas , el dominio se refiere al conjunto de valores de entrada (valores x) para los que se define la función, y el rango se refiere al conjunto de valores de salida (valores y) que la función puede tomar.
Aquí están los dominios y rangos de las seis funciones trigonométricas inversas:
| Rango | de dominio | de función |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |