شش تابع مثلثاتی sin، cos، tan، cosec، sec و cot هستند.
اجازه دهید سعی کنیم \(\angle A\) در مثلث داده شده پیدا کنیم.
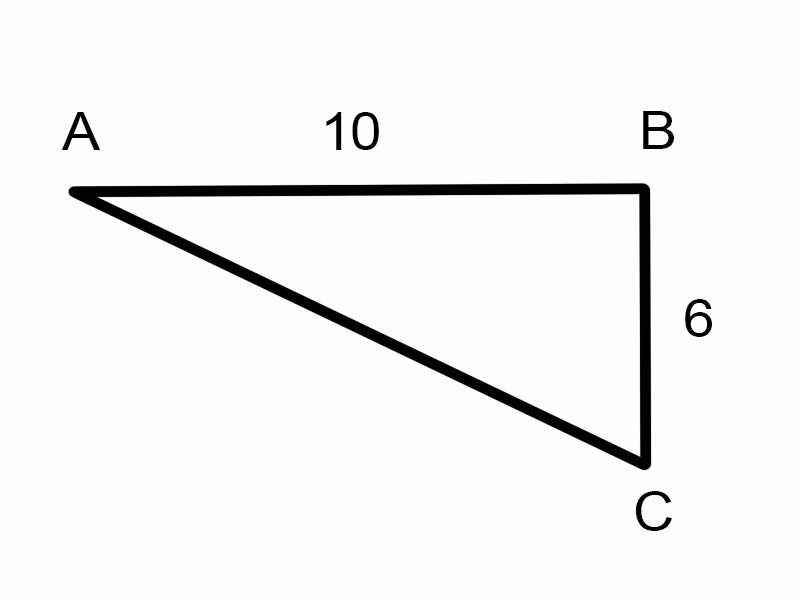
\(\tan A = \frac{6}{10}\)
اما این برای یافتن اندازه \(\angle A\) مفید نیست.
ما باید یک ابزار ریاضی جدید برای حل مسائلی از این دست پیدا کنیم. توابع سینوس، کسینوس و مماس زاویه می گیرند و نسبت ضلعی می دهند. اما ما به توابعی نیاز داریم که نسبت اضلاع را بگیرند و زاویه دهند و بنابراین توابع مثلثاتی معکوس معرفی شوند.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96 درجه [ارزیابی با ماشین حساب]
اگر طول دو ضلع مشخص باشد، اندازه گیری زاویه را می توان با استفاده از تابع مثلثاتی معکوس تعیین کرد.
\(\sin^{-1}x \textrm{ یا } \arcsin x\) تابع سینوس معکوس است.
\(\cos^{-1}x \textrm{ یا } \arccos x \) تابع cos معکوس است.
\(\tan^{-1}x \textrm{ یا } \arctan x\) تابع tan معکوس است.
\(\csc^{-1}x \) یا arccsc x تابع csc معکوس است.
\(\sec^{-1}x \) یا arcsec x تابع ثانیه معکوس است.
\(cot^{-1}x \) یا arccot x تابع cot معکوس است.
در یک مثلث اجازه دهید \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [به عنوان \(\sin\theta = \) عمود∕ Hypotenuse]
می توانیم به صورت \({x \over 1} = \frac{AB}{AC}\) بنویسیم
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
وقتی \(\theta\) مطابق جدول زیر به صورت معکوس داده می شود، می توانیم مقدار نسبت های مثلثاتی را استخراج کنیم :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
مثال 1: یک نردبان به دیوار تکیه داده و با زمین زاویه θ ایجاد می کند. فاصله پایه نردبان از دیوار 3 متر و طول نردبان 5 متر است. θ را پیدا کنید.
راه حل:
از آنجایی که ما هیپوتنوس (5 متر) و ضلع مجاور (3 متر) داریم، از تابع کسینوس استفاده می کنیم:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) از ماشین حساب برای استخراج مقدار θ, \(\theta \approx 53.13^{\circ}\) استفاده کنید
مثال 2: ارزشیابی \(cos^{−1}(\frac{-1}{2}) \)
راه حل:
با استفاده از ویژگی بازتاب: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
جایگزینی \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
مثال 3: \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \) را ارزیابی کنید
راه حل:
با استفاده از هویت: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
در توابع مثلثاتی معکوس ، دامنه به مجموعه مقادیر ورودی (مقدار x) که تابع برای آن تعریف شده است، اشاره دارد، و محدوده به مجموعه مقادیر خروجی (مقادیر y) اشاره دارد که تابع می تواند بگیرد.
در اینجا دامنه ها و محدوده های شش تابع مثلثاتی معکوس آمده است:
| تابع | دامنه | دامنه |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |