Les six fonctions trigonométriques sont sin, cos, tan, cosec, sec et cot.
Essayons de trouver \(\angle A\) dans le triangle donné.
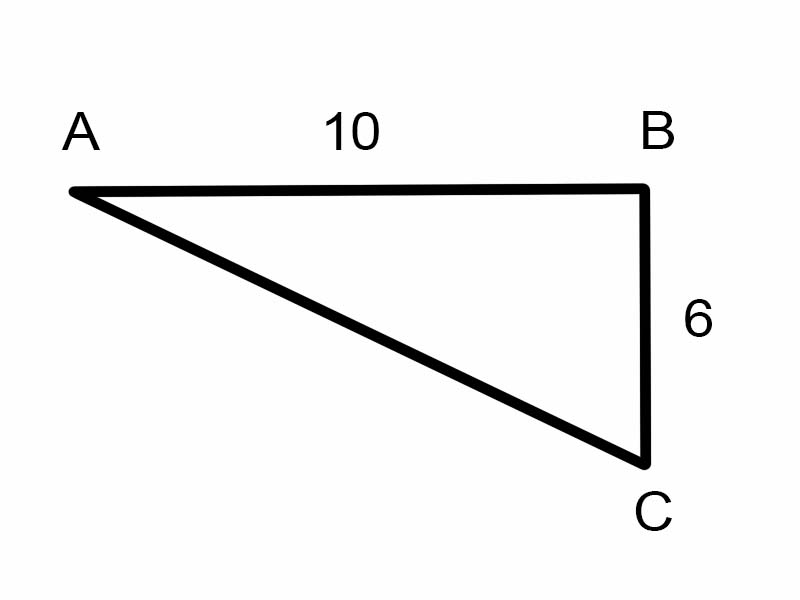
\(\tan A = \frac{6}{10}\)
Mais cela n'est pas utile pour trouver la mesure de \(\angle A\)
Nous devons trouver un nouvel outil mathématique pour résoudre des problèmes comme ceux-ci. Les fonctions sinus, cosinus et tangente prennent des angles et donnent des rapports latéraux. Mais nous avons besoin de fonctions qui prennent des rapports latéraux et donnent des angles et donc des fonctions trigonométriques inverses sont introduites.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Évaluer avec la calculatrice]
Si la longueur des deux côtés est connue, les mesures d'angle peuvent être déterminées à l'aide de la fonction trigonométrique inverse.
\(\sin^{-1}x \textrm{ ou } \arcsin x\) est une fonction sinus inverse.
\(\cos^{-1}x \textrm{ ou } \arccos x \) est une fonction cos inverse.
\(\tan^{-1}x \textrm{ ou } \arctan x\) est la fonction tan inverse.
\(\csc^{-1}x \) ou arccsc x est une fonction csc inverse.
\(\sec^{-1}x \) ou arcsec x est la fonction sec inverse.
\(cot^{-1}x \) ou arccot x est la fonction cot inverse.
Dans un triangle soit \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [comme \(\sin\theta = \) Perpendiculaire∕ Hypoténuse]
On peut écrire comme \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Nous pouvons dériver la valeur des rapports trigonométriques lorsque \(\theta\) est donné comme inverse selon le tableau ci-dessous :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Exemple 1 : Une échelle est appuyée contre un mur, formant un angle θ avec le sol. La base de l'échelle est à 3 mètres du mur et l'échelle mesure 5 mètres de long. Trouvez θ.
Solution:
Puisque nous avons l'hypoténuse (5 m) et le côté adjacent (3 m), nous utilisons la fonction cosinus :
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Utilisez la calculatrice pour dériver la valeur de θ, \(\theta \approx 53.13^{\circ}\)
Exemple 2 : Évaluer \(cos^{−1}(\frac{-1}{2}) \)
Solution:
En utilisant la propriété de réflexion : \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
En remplaçant \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Exemple 3 : Évaluer \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Solution:
En utilisant l'identité : \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Dans les fonctions trigonométriques inverses , le domaine fait référence à l'ensemble des valeurs d'entrée (valeurs x) pour lesquelles la fonction est définie, et la plage fait référence à l'ensemble des valeurs de sortie (valeurs y) que la fonction peut prendre.
Voici les domaines et les plages des six fonctions trigonométriques inverses :
| Plage | de domaine | de fonction |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |