छह त्रिकोणमितीय फलन sin, cos, tan, cosec, sec और cot हैं।
आइए दिए गए त्रिभुज में \(\angle A\) ज्ञात करने का प्रयास करें।
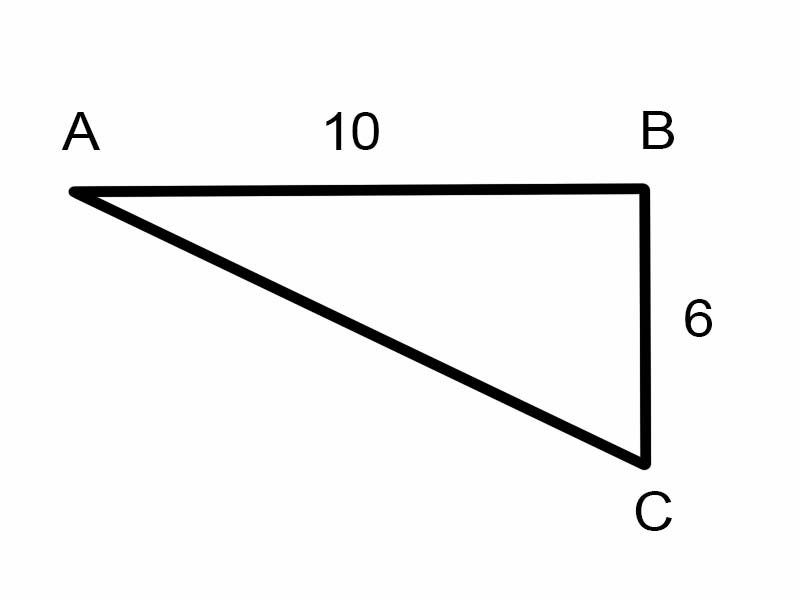
\(\tan A = \frac{6}{10}\)
लेकिन यह \(\angle A\) का माप ज्ञात करने में सहायक नहीं है
हमें ऐसी समस्याओं को हल करने के लिए एक नया गणितीय उपकरण खोजने की आवश्यकता है। साइन, कोसाइन और टेंगेंट फ़ंक्शन कोण लेते हैं और साइड अनुपात देते हैं। लेकिन हमें ऐसे फ़ंक्शन की आवश्यकता है जो साइड अनुपात लेते हैं और कोण देते हैं और इसलिए व्युत्क्रम त्रिकोणमितीय फ़ंक्शन पेश किए जाते हैं।
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [कैलकुलेटर से मूल्यांकन करें]
यदि दो भुजाओं की लंबाई ज्ञात हो, तो व्युत्क्रम त्रिकोणमितीय फलन का उपयोग करके कोण माप निर्धारित किया जा सकता है।
\(\sin^{-1}x \textrm{ या } \arcsin x\) व्युत्क्रम साइन फ़ंक्शन है।
\(\cos^{-1}x \textrm{ या } \arccos x \) व्युत्क्रम cos फ़ंक्शन है।
\(\tan^{-1}x \textrm{ या } \arctan x\) व्युत्क्रम tan फ़ंक्शन है।
\(\csc^{-1}x \) या arccsc x व्युत्क्रम csc फ़ंक्शन है।
\(\sec^{-1}x \) या आर्कसेक x व्युत्क्रम सेक फ़ंक्शन है।
\(cot^{-1}x \) या arccot x व्युत्क्रम cot फ़ंक्शन है।
एक त्रिभुज में मान लीजिए \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [चूँकि \(\sin\theta = \) लंबवत∕ कर्ण]
हम इसे इस प्रकार लिख सकते हैं \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
जब \(\theta\) को व्युत्क्रम के रूप में दिया जाता है तो हम त्रिकोणमितीय अनुपातों का मान नीचे दी गई तालिका के अनुसार प्राप्त कर सकते हैं :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
उदाहरण 1: एक सीढ़ी दीवार के सहारे टिकी हुई है, जो ज़मीन के साथ θ कोण बना रही है। सीढ़ी का आधार दीवार से 3 मीटर दूर है, और सीढ़ी 5 मीटर लंबी है। θ ज्ञात करें।
समाधान:
चूँकि हमारे पास कर्ण (5 मीटर) और आसन्न भुजा (3 मीटर) है, हम कोसाइन फ़ंक्शन का उपयोग करते हैं:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) θ का मान निकालने के लिए कैलकुलेटर का उपयोग करें, \(\theta \approx 53.13^{\circ}\)
उदाहरण 2: \(cos^{−1}(\frac{-1}{2}) \) मूल्यांकन करें
समाधान:
परावर्तन गुण का उपयोग करके: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\( x=\frac{1}{2} \) प्रतिस्थापित करने पर
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
उदाहरण 3: \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \) मूल्यांकन करें
समाधान:
पहचान का उपयोग करते हुए: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
व्युत्क्रम त्रिकोणमितीय फ़ंक्शनों में, डोमेन इनपुट मानों (x-मानों) के सेट को संदर्भित करता है जिसके लिए फ़ंक्शन परिभाषित किया गया है, और रेंज आउटपुट मानों (y-मानों) के सेट को संदर्भित करता है जिसे फ़ंक्शन ले सकता है।
यहां छह व्युत्क्रम त्रिकोणमितीय फलनों के डोमेन और परिसर दिए गए हैं:
| फ़ंक्शन | डोमेन | रेंज |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |