Šest trigonometrijskih funkcija su sin, cos, tan, cosec, sec i cot.
Pokušajmo pronaći \(\angle A\) u zadanom trokutu.
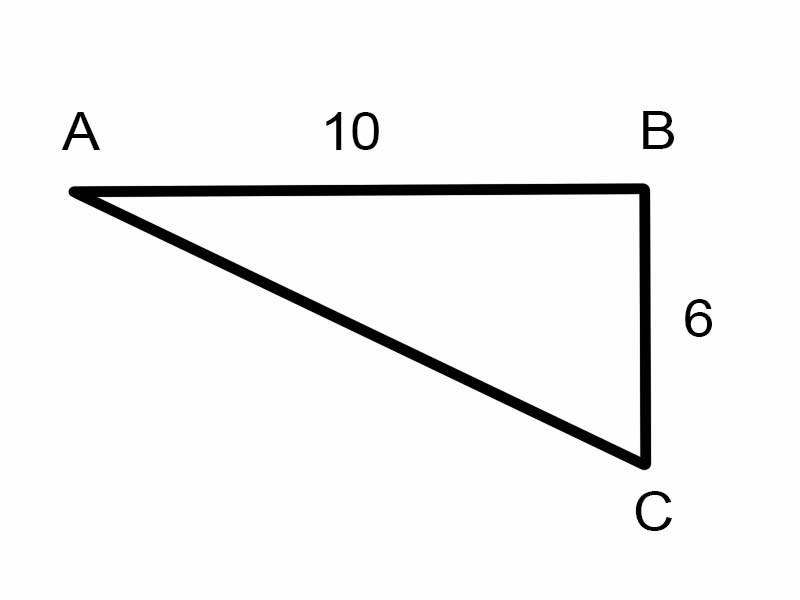
\(\tan A = \frac{6}{10}\)
Ali ovo nije od pomoći za pronalaženje mjere \(\angle A\)
Moramo pronaći novi matematički alat za rješavanje ovakvih problema. Funkcije sinusa, kosinusa i tangensa uzimaju kutove i daju omjere stranica. Ali trebamo funkcije koje uzimaju omjere stranica i daju kutove i stoga se uvode inverzne trigonometrijske funkcije .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Procijenite kalkulatorom]
Ako je poznata duljina dviju stranica, mjere kuta mogu se odrediti pomoću inverzne trigonometrijske funkcije.
\(\sin^{-1}x \textrm{ ili } \arcsin x\) je inverzna sinusna funkcija.
\(\cos^{-1}x \textrm{ ili } \arccos x \) je inverzna cos funkcija.
\(\tan^{-1}x \textrm{ ili } \arctan x\) je inverzna tan funkcija.
\(\csc^{-1}x \) ili arccsc x je inverzna csc funkcija.
\(\sec^{-1}x \) ili arcsec x je inverzna sek funkcija.
\(cot^{-1}x \) ili arccot x je inverzna cot funkcija.
Neka u trokutu \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [kao \(\sin\theta = \) okomica∕ hipotenuza]
Možemo pisati kao \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Možemo izvesti vrijednost trigonometrijskih omjera kada je \(\theta\) dan kao inverz prema donjoj tablici :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Primjer 1: Ljestve su naslonjene na zid, čineći kut θ s tlom. Podnožje ljestvi udaljeno je 3 metra od zida, a ljestve su dugačke 5 metara. Nađi θ.
Otopina:
Budući da imamo hipotenuzu (5 m) i susjednu stranicu (3 m), koristimo funkciju kosinusa:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Koristite kalkulator za izvođenje vrijednosti θ, \(\theta \approx 53.13^{\circ}\)
Primjer 2: Izračunajte \(cos^{−1}(\frac{-1}{2}) \)
Otopina:
Korištenje svojstva refleksije: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Zamjena \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Primjer 3: Izračunajte \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Otopina:
Korištenje identiteta: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
U inverznim trigonometrijskim funkcijama , domena se odnosi na skup ulaznih vrijednosti (x-vrijednosti) za koje je funkcija definirana, a raspon se odnosi na skup izlaznih vrijednosti (y-vrijednosti) koje funkcija može uzeti.
Ovdje su domene i rasponi šest inverznih trigonometrijskih funkcija:
| Raspon | domene | funkcije |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |