Enam fungsi trigonometri adalah sin, cos, tan, cosec, sec dan cot.
Mari kita coba mencari \(\angle A\) dalam segitiga yang diberikan.
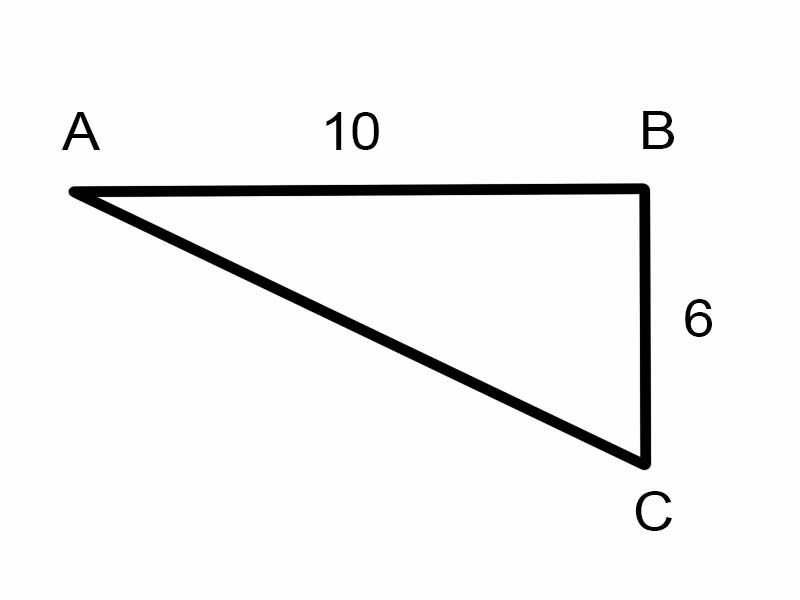
\(\tan A = \frac{6}{10}\)
Namun hal ini tidak membantu untuk menemukan ukuran \(\angle A\)
Kita perlu menemukan alat matematika baru untuk memecahkan masalah seperti ini. Fungsi Sinus, Kosinus, dan Tangen mengambil sudut dan memberikan rasio sisi. Namun, kita memerlukan fungsi yang mengambil rasio sisi dan memberikan sudut, oleh karena itu fungsi Trigonometri Invers diperkenalkan.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Evaluasi dengan kalkulator]
Jika panjang dua sisi diketahui, ukuran sudut dapat ditentukan menggunakan fungsi trigonometri invers.
\(\sin^{-1}x \textrm{ atau } \arcsin x\) adalah fungsi sinus invers.
\(\cos^{-1}x \textrm{ atau } \arccos x \) adalah fungsi cos invers.
\(\tan^{-1}x \textrm{ atau } \arctan x\) adalah fungsi tan invers.
\(\csc^{-1}x \) atau arccsc x adalah fungsi csc invers.
\(\sec^{-1}x \) atau arcsec x adalah fungsi invers sec.
\(cot^{-1}x \) atau arccot x adalah fungsi cot invers.
Dalam sebuah segitiga misalkan \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [karena \(\sin\theta = \) tegak lurus∕ sisi miring]
Kita dapat menuliskannya sebagai \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Kita dapat memperoleh nilai rasio trigonometri ketika \(\theta\) diberikan sebagai invers sesuai tabel di bawah ini :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
Persamaan kuadrat terkecil adalah \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Contoh 1: Sebuah tangga bersandar pada dinding dan membentuk sudut θ dengan tanah. Alas tangga berjarak 3 meter dari dinding, dan panjang tangga 5 meter. Carilah θ.
Larutan:
Karena kita memiliki sisi miring (5 m) dan sisi yang berdekatan (3 m), kita menggunakan fungsi kosinus:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Gunakan kalkulator untuk mendapatkan nilai θ, \(\theta \approx 53.13^{\circ}\)
Contoh 2: Evaluasi \(cos^{−1}(\frac{-1}{2}) \)
Larutan:
Menggunakan sifat refleksi: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Mengganti \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Contoh 3: Evaluasi \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Larutan:
Menggunakan identitas: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Dalam fungsi trigonometri invers , domain merujuk pada himpunan nilai masukan (nilai-x) yang menjadi definisi fungsi tersebut, dan range merujuk pada himpunan nilai keluaran (nilai-y) yang dapat diambil oleh fungsi tersebut.
Berikut adalah domain dan rentang dari enam fungsi trigonometri invers:
| Rentang | Domain | Fungsi |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |