Le sei funzioni trigonometriche sono seno, coseno, tangente, cosec, sec e cot.
Proviamo a trovare \(\angle A\) nel triangolo dato.
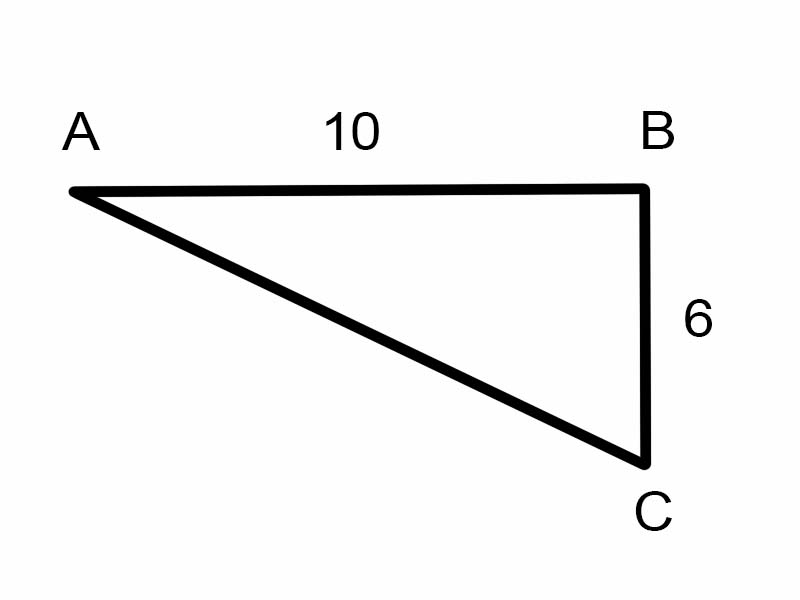
\(\tan A = \frac{6}{10}\)
Ma questo non è utile per trovare la misura dell \(\angle A\)
Dobbiamo trovare un nuovo strumento matematico per risolvere problemi come questi. Le funzioni seno, coseno e tangente prendono angoli e danno rapporti laterali. Ma abbiamo bisogno di funzioni che prendano rapporti laterali e diano angoli e quindi vengono introdotte le funzioni trigonometriche inverse .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Valutare con la calcolatrice]
Se è nota la lunghezza di due lati, è possibile determinare le misure degli angoli utilizzando la funzione trigonometrica inversa.
\(\sin^{-1}x \textrm{ O } \arcsin x\) è la funzione seno inversa.
\(\cos^{-1}x \textrm{ O } \arccos x \) è la funzione coseno inversa.
\(\tan^{-1}x \textrm{ O } \arctan x\) è la funzione tangente inversa.
\(\csc^{-1}x \) o arccsc x è la funzione csc inversa.
\(\sec^{-1}x \) o arcsec x è la funzione sec inversa.
\(cot^{-1}x \) o arccot x è la funzione cot inversa.
In un triangolo sia \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [come \(\sin\theta = \) Perpendicolare ∕ Ipotenusa]
Possiamo scrivere come \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Possiamo ricavare il valore dei rapporti trigonometrici quando \(\theta\) è dato come inverso secondo la tabella seguente :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Esempio 1: Una scala è appoggiata a un muro, formando un angolo θ con il terreno. La base della scala è a 3 metri di distanza dal muro e la scala è lunga 5 metri. Trova θ.
Soluzione:
Poiché abbiamo l'ipotenusa (5 m) e il lato adiacente (3 m), utilizziamo la funzione coseno:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Utilizzare la calcolatrice per ricavare il valore di θ, \(\theta \approx 53.13^{\circ}\)
Esempio 2: Valutare \(cos^{−1}(\frac{-1}{2}) \)
Soluzione:
Utilizzando la proprietà di riflessione: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Sostituendo \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Esempio 3: Valutare \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Soluzione:
Utilizzando l'identità: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Nelle funzioni trigonometriche inverse , il dominio si riferisce all'insieme dei valori di input (valori x) per i quali la funzione è definita, mentre l' intervallo si riferisce all'insieme dei valori di output (valori y) che la funzione può assumere.
Ecco i domini e gli intervalli delle sei funzioni trigonometriche inverse:
| Funzione | Dominio | Intervallo |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |