6 つの三角関数は sin、cos、tan、cosec、sec、cot です。
与えられた三角形の中で\(\angle A\)を見つけてみましょう。
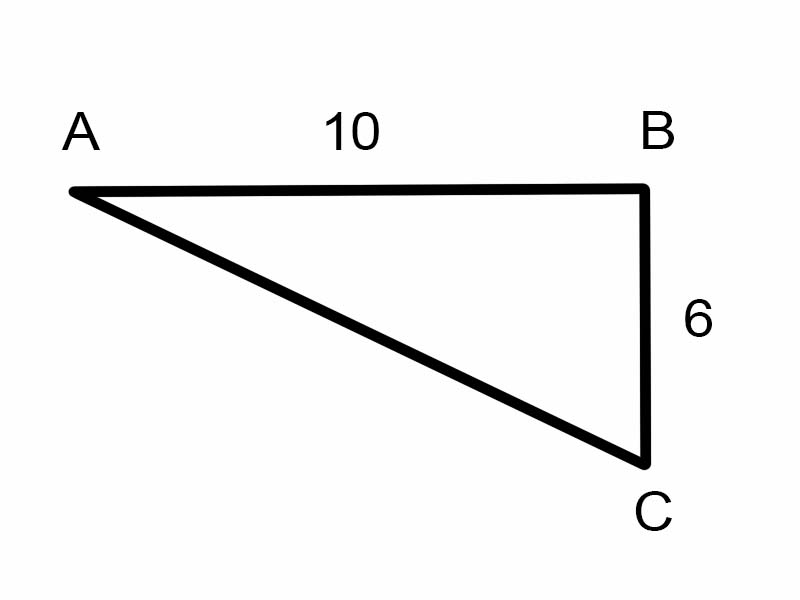
\(\tan A = \frac{6}{10}\)
しかし、これは\(\angle A\)の測定値を見つけるのに役立ちません。
このような問題を解決するには、新しい数学的なツールを見つける必要があります。正弦関数、余弦関数、正接関数は角度を取り、辺の比を与えます。しかし、辺の比を取り、角度を与える関数が必要なので、逆三角関数が導入されます。
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [計算機で計算]
2 辺の長さがわかっている場合は、逆三角関数を使用して角度の測定値を決定できます。
\(\sin^{-1}x \textrm{ または } \arcsin x\)逆正弦関数です。
\(\cos^{-1}x \textrm{ または } \arccos x \)逆cos関数です。
\(\tan^{-1}x \textrm{ または } \arctan x\)逆正接関数です。
\(\csc^{-1}x \)または arccsc x は逆 csc 関数です。
\(\sec^{-1}x \)または arcsec x は逆 sec 関数です。
\(cot^{-1}x \)または arccot x は逆 cot 関数です。
三角形では\(\sin \theta = x\)とします。
⇒ \(\sin \theta = {x \over 1}\) [ \(\sin\theta = \)垂線∕ 斜辺として]
\({x \over 1} = \frac{AB}{AC}\)と書くことができます。
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
\(\theta\)以下の表に従って逆数として与えられた場合、三角比の値を導くことができます。
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
例 1: はしごが壁に立てかけられ、地面と角度 θ をなしています。はしごの土台は壁から 3 メートル離れており、はしごの長さは 5 メートルです。θ を求めます。
解決:
斜辺(5 m)と隣接辺(3 m)があるので、余弦関数を使用します。
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\)計算機を使用して θ の値を導出します。 \(\theta \approx 53.13^{\circ}\)
例2: \(cos^{−1}(\frac{-1}{2}) \)を評価する
解決:
反射特性を使用する: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\( x=\frac{1}{2} \)を代入すると
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
例3: \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)を評価する
解決:
等式を使用する: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
逆三角関数では、定義域は関数が定義される入力値 (x 値) のセットを指し、範囲は関数が取ることのできる出力値 (y 値) のセットを指します。
6 つの逆三角関数の定義域と値域は次のとおりです。
| 関数 | 領域の | 範囲 |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) 、 \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) 、 \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |