Шесте тригонометриски функции се sin, cos, tan, cosec, sec и cot.
Ајде да се обидеме да најдеме \(\angle A\) во дадениот триаголник.
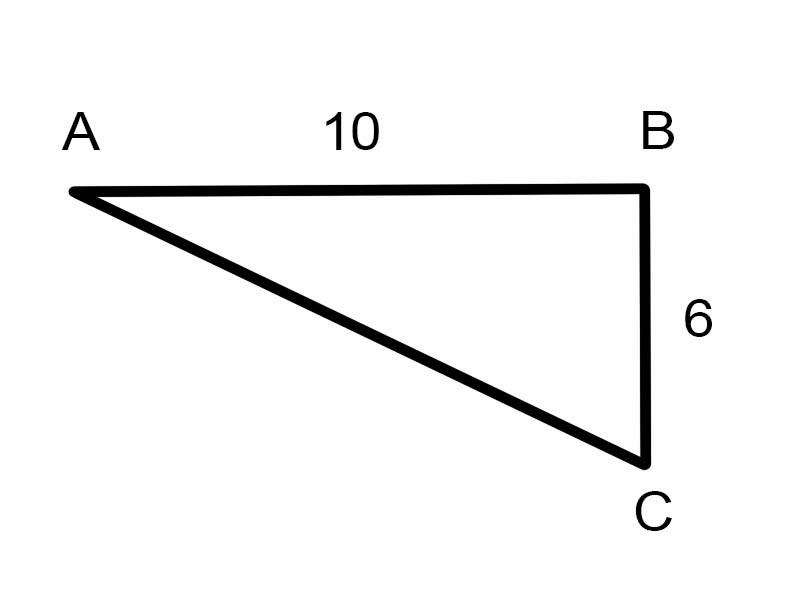
\(\tan A = \frac{6}{10}\)
Но, ова не е корисно да се најде мерката за \(\angle A\)
Треба да најдеме нова математичка алатка за да решаваме проблеми како овие. Функциите синус, косинус и тангента заземаат агли и даваат странични соодноси. Но, потребни ни се функции кои земаат странични соодноси и даваат агли и затоа се воведуваат инверзни тригонометриски функции .
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Оценете со калкулаторот]
Ако се знае должината на двете страни, мерилата на аголот може да се одредат со помош на инверзна тригонометриска функција.
\(\sin^{-1}x \textrm{ или } \arcsin x\) е инверзна синусна функција.
\(\cos^{-1}x \textrm{ или } \arccos x \) е инверзна cos функција.
\(\tan^{-1}x \textrm{ или } \arctan x\) е инверзна тен функција.
\(\csc^{-1}x \) или arccsc x е инверзна csc функција.
\(\sec^{-1}x \) или arcsec x е инверзна сек функција.
\(cot^{-1}x \) или arccot x е инверзна функција на креветчето.
Во триаголник нека \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [како \(\sin\theta = \) Перпендикуларна∕ хипотенуза]
Можеме да напишеме како \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Можеме да изведеме вредност на тригонометриските соодноси кога \(\theta\) е дадена како инверзна според табелата подолу :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Пример 1: Скала се потпира на ѕид, правејќи агол θ со земјата. Основата на скалата е оддалечена 3 метри од ѕидот, а скалата е долга 5 метри. Најдете θ.
Решение:
Бидејќи ја имаме хипотенузата (5 m) и соседната страна (3 m), ја користиме функцијата косинус:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Користете калкулатор за да ја изведете вредноста на θ, \(\theta \approx 53.13^{\circ}\)
Пример 2: Оценете \(cos^{−1}(\frac{-1}{2}) \)
Решение:
Користење на својството за рефлексија: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Замена на \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Пример 3: Оценете \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Решение:
Користејќи го идентитетот: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Кај инверзните тригонометриски функции , доменот се однесува на множеството на влезни вредности (x-вредности) за кои е дефинирана функцијата, а опсегот се однесува на множеството излезни вредности (y-вредности) што функцијата може да ги земе.
Еве ги домените и опсезите на шесте инверзни тригонометриски функции:
| Опсег на | домен | на функција |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(-\infty \le x \le \infty\) | \(y = \cot^{-1}x\) | \(0 \lt y \lt {\pi}\) |