Тригонометрийн зургаан функц нь sin, cos, tan, cosec, sec, cot юм.
Өгөгдсөн гурвалжин дотроос \(\angle A\) олохыг оролдъё.
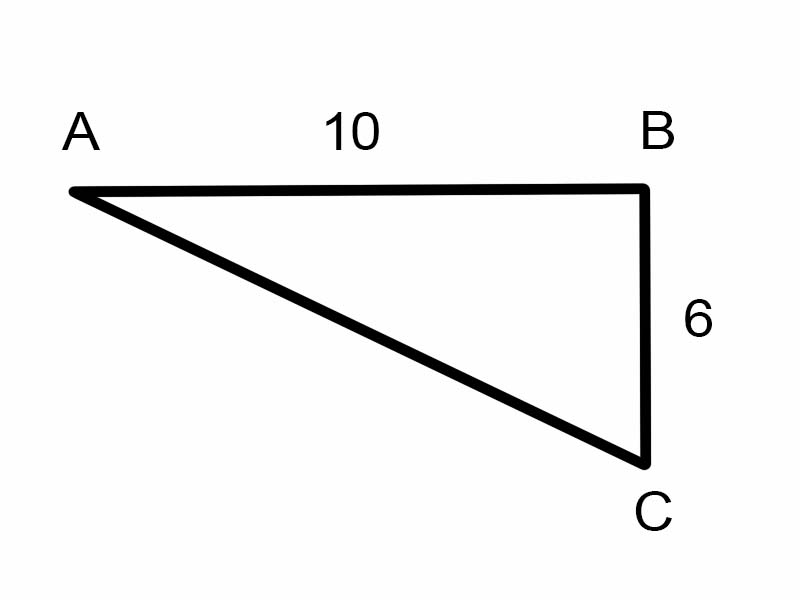
\(\tan A = \frac{6}{10}\)
Гэхдээ энэ нь \(\angle A\) хэмжигдэхүүнийг олоход тус болохгүй.
Иймэрхүү асуудлыг шийдэхийн тулд бид математикийн шинэ хэрэгсэл олох хэрэгтэй. Синус, косинус, тангенс функцууд нь өнцгийг авч, хажуугийн харьцааг өгдөг. Гэхдээ бидэнд хажуугийн харьцаа, өнцгийг өгдөг функц хэрэгтэй байгаа тул урвуу тригонометрийн функцүүдийг танилцуулж байна.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [Тооцоологчоор үнэлэх]
Хэрэв хоёр талын урт нь мэдэгдэж байгаа бол урвуу тригонометрийн функцийг ашиглан өнцгийн хэмжүүрийг тодорхойлж болно.
\(\sin^{-1}x \textrm{ эсвэл } \arcsin x\) нь урвуу синусын функц юм.
\(\cos^{-1}x \textrm{ эсвэл } \arccos x \) нь урвуу cos функц юм.
\(\tan^{-1}x \textrm{ эсвэл } \arctan x\) нь урвуу tan функц юм.
\(\csc^{-1}x \) эсвэл arccsc x нь урвуу csc функц юм.
\(\sec^{-1}x \) эсвэл arcsec x нь урвуу сек функц юм.
\(cot^{-1}x \) эсвэл arccot x нь урвуу ор функц юм.
Гурвалжинд \(\sin \theta = x\) гэж бичье.
⇒ \(\sin \theta = {x \over 1}\) [ \(\sin\theta = \) Перпендикуляр∕ Гипотенуз]
Бид \({x \over 1} = \frac{AB}{AC}\) гэж бичиж болно.
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
Дараах хүснэгтийн дагуу \(\theta\) урвуу байдлаар өгөгдсөн үед бид тригонометрийн харьцааны утгыг гаргаж болно .
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Жишээ 1: Шат хананд налж, газартай θ өнцөг үүсгэв. Шатны суурь нь хананаас 3 метрийн зайтай, шат нь 5 метр урттай. θ олох.
Шийдэл:
Гипотенуз (5 м) ба зэргэлдээ тал (3 м) байгаа тул бид косинусын функцийг ашигладаг.
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Тооцоологч ашиглан θ, \(\theta \approx 53.13^{\circ}\) ийн утгыг гаргана уу.
Жишээ 2: Үнэлгээ хийх \(cos^{−1}(\frac{-1}{2}) \)
Шийдэл:
Тусгалын шинж чанарыг ашиглан: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\( x=\frac{1}{2} \) орлуулж байна
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Жишээ 3: Үнэлгээ хийх \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Шийдэл:
Идентификаторыг ашиглан: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Урвуу тригонометрийн функцүүдэд домэйн нь тухайн функцийг тодорхойлсон оролтын утгуудын багцыг (x-утгууд), муж нь функцийн авч чадах гаралтын утгуудын багцыг (y-утгууд) хэлнэ.
Урвуу тригонометрийн зургаан функцын домэйн ба мужууд энд байна.
| Функцийн | домайн | хүрээ |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) их, |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |