trigonometric function ခြောက်ခုမှာ sin, cos, tan, cosec, sec နှင့် cot တို့ဖြစ်သည်။
ပေးထားသော တြိဂံတွင် \(\angle A\) ကို ရှာကြည့်ကြပါစို့။
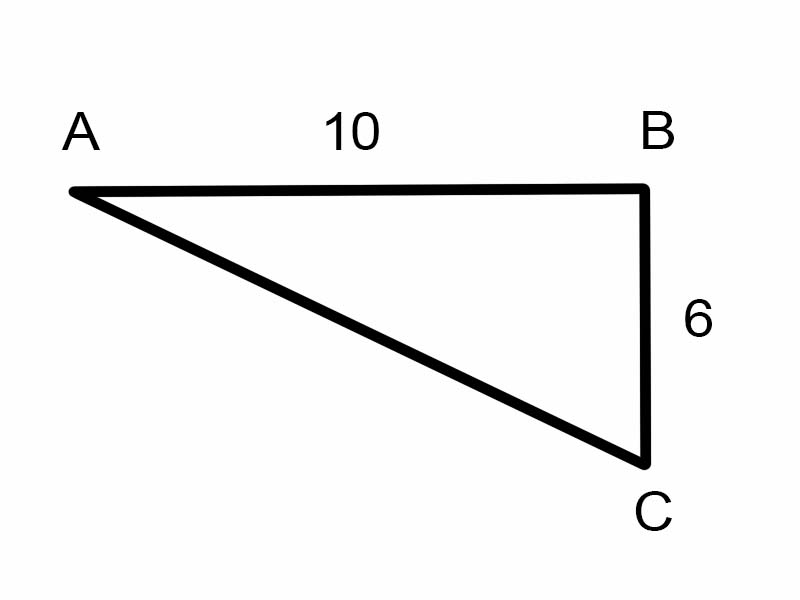
\(\tan A = \frac{6}{10}\)
သို့သော် \(\angle A\) ၏ အတိုင်းအတာကို ရှာရန် ၎င်းသည် အထောက်အကူ မဖြစ်ပါ။
ဤကဲ့သို့သော ပြဿနာများကို ဖြေရှင်းရန် သင်္ချာကိရိယာအသစ်ကို ကျွန်ုပ်တို့ ရှာဖွေရန် လိုအပ်ပါသည်။ Sine၊ Cosine နှင့် Tangent လုပ်ဆောင်ချက်များသည် ထောင့်များကိုယူ၍ ဘေးထွက်အချိုးများကို ပေးသည်။ သို့သော် ကျွန်ုပ်တို့သည် ဘေးထွက်အချိုးများနှင့် ထောင့်များကိုပေးသည့် လုပ်ဆောင်ချက်များ လိုအပ်ပြီး ထို့ကြောင့် Inverse Trigonometric လုပ်ဆောင်ချက်များကို မိတ်ဆက်ပေးပါသည်။
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30.96° [ဂဏန်းပေါင်းစက်ဖြင့် အကဲဖြတ်ပါ]
အကယ်၍ ဘေးနှစ်ဖက်၏ အရှည်ကို သိပါက၊ ပြောင်းပြန် trigonometric လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ထောင့်တိုင်းတာမှုများကို ဆုံးဖြတ်နိုင်သည်။
\(\sin^{-1}x \textrm{ သို့မဟုတ် } \arcsin x\) သည် inverse sine function ဖြစ်သည်။
\(\cos^{-1}x \textrm{ သို့မဟုတ် } \arccos x \) သည် inverse cos လုပ်ဆောင်ချက် ဖြစ်သည်။
\(\tan^{-1}x \textrm{ သို့မဟုတ် } \arctan x\) သည် inverse tan function ဖြစ်သည်။
\(\csc^{-1}x \) သို့မဟုတ် arccsc x သည် ပြောင်းပြန် csc လုပ်ဆောင်ချက် ဖြစ်သည်။
\(\sec^{-1}x \) သို့မဟုတ် arcsec x သည် စက္ကန့်ပြောင်းပြန် လုပ်ဆောင်ချက် ဖြစ်သည်။
\(cot^{-1}x \) သို့မဟုတ် arccot x သည် ပြောင်းပြန် cot လုပ်ဆောင်ချက်ဖြစ်သည်။
တြိဂံတစ်ခုတွင် \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [as \(\sin\theta = \) Perpendicular∕ Hypotenuse]
\({x \over 1} = \frac{AB}{AC}\) အဖြစ် ရေးနိုင်သည်။
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
အောက်ဖော်ပြပါဇယားအရ \(\theta\) ပြောင်းပြန်အဖြစ်ပေးသောအခါ trigonometric အချိုး၏တန်ဖိုးကို ရယူနိုင်သည် -
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
ဥပမာ 1- လှေကားသည် နံရံကိုမှီ၍ မြေနှင့်ထောင့် θ လုပ်သည်။ လှေခါး၏ခြေရင်းသည် နံရံမှ ၃ မီတာအကွာတွင်ရှိပြီး လှေခါးသည် ၅ မီတာရှည်သည်။ θ ရှာပါ။
ဖြေရှင်းချက်-
ကျွန်ုပ်တို့တွင် hypotenuse (5 m) နှင့် ကပ်လျက်ဘက် (3 m) ရှိသောကြောင့်၊ ကျွန်ုပ်တို့သည် cosine function ကိုအသုံးပြုသည်-
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) θ တန်ဖိုးကို ရယူရန် ဂဏန်းပေါင်းစက်ကို အသုံးပြုပါ၊ \(\theta \approx 53.13^{\circ}\)
ဥပမာ 2- \(cos^{−1}(\frac{-1}{2}) \) အကဲဖြတ်ပါ
ဖြေရှင်းချက်-
ရောင်ပြန်ဟပ်မှု ပိုင်ဆိုင်မှုကို အသုံးပြုခြင်း \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
အစားထိုးခြင်း \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
ဥပမာ 3- အကဲဖြတ်ပါ \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
ဖြေရှင်းချက်-
အထောက်အထားကို အသုံးပြုခြင်း \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
ပြောင်းပြန်ထရီဂိုနိုမက်ထရစ်လုပ်ဆောင်ချက်များ တွင်၊ ဒိုမိန်းသည် လုပ်ဆောင်ချက်ကိုသတ်မှတ်ထားသည့် input တန်ဖိုးများ (x-values) အစုအဝေးကို ရည်ညွှန်းပြီး အကွာအဝေးသည် လုပ်ဆောင်နိုင်သော အထွက်တန်ဖိုးများ (y-တန်ဖိုးများ) ကို ရည်ညွှန်းသည်။
ဤသည်မှာ ပြောင်းပြန် trigonometric လုပ်ဆောင်ချက် ခြောက်ခု၏ ဒိုမိန်းများနှင့် အပိုင်းအခြားများဖြစ်သည်-
| Function | Domain | Range |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |