छ त्रिकोणमितीय कार्यहरू sin, cos, tan, cosec, sec र cot हुन्।
दिइएको त्रिभुजमा \(\angle A\) खोज्ने प्रयास गरौं।
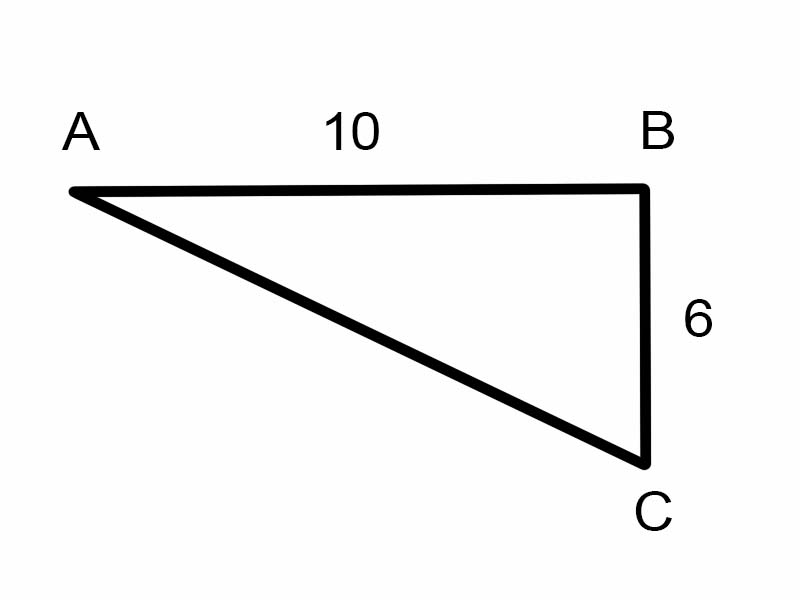
\(\tan A = \frac{6}{10}\)
तर यो \(\angle A\) को नाप पत्ता लगाउन उपयोगी छैन।
यस्ता समस्याहरू समाधान गर्न हामीले नयाँ गणितीय उपकरण खोज्नु पर्छ। साइन, कोसाइन र ट्यान्जेन्ट प्रकार्यहरूले कोणहरू लिन्छ र तर्फ अनुपात दिन्छ। तर हामीलाई तर्फ अनुपात लिने र तर्फ कोण दिने प्रकार्यहरू चाहिन्छ र त्यसैले व्युत्क्रम त्रिकोणमितीय प्रकार्यहरू प्रस्तुत गरिन्छ।
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = ३०.९६° [क्याल्कुलेटरको साथ मूल्याङ्कन गर्नुहोस्]
यदि दुई भुजाहरूको लम्बाइ थाहा छ भने, व्युत्क्रम त्रिकोणमितीय प्रकार्य प्रयोग गरेर कोण मापन निर्धारण गर्न सकिन्छ।
\(\sin^{-1}x \textrm{ वा } \arcsin x\) व्युत्क्रम साइन प्रकार्य हो।
\(\cos^{-1}x \textrm{ वा } \arccos x \) उल्टो cos प्रकार्य हो।
\(\tan^{-1}x \textrm{ वा } \arctan x\) व्युत्क्रम tan प्रकार्य हो।
\(\csc^{-1}x \) वा arccsc x उल्टो csc प्रकार्य हो।
\(\sec^{-1}x \) वा arcsec x भनेको inverse sec प्रकार्य हो।
\(cot^{-1}x \) वा arccot x भनेको inverse cot प्रकार्य हो।
त्रिभुजमा मानौं \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [जस्तै \(\sin\theta = \) लम्ब∕ कर्ण]
हामी \({x \over 1} = \frac{AB}{AC}\) लेख्न सक्छौं।
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
तलको तालिका अनुसार \(\theta\) लाई व्युत्क्रम दिइएको खण्डमा हामी त्रिकोणमितीय अनुपातको मान निकाल्न सक्छौं :
१. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
२. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
३. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
उदाहरण १: एउटा भर्याङ भित्तामा अडिएको छ, जसले गर्दा जमिनसँग θ कोण बनाइएको छ। भर्याङको आधार भित्ताबाट ३ मिटर टाढा छ, र भर्याङ ५ मिटर लामो छ। θ पत्ता लगाउनुहोस्।
समाधान:
हामीसँग कर्ण (५ मिटर) र छेउछाउको पक्ष (३ मिटर) भएकोले, हामी कोसाइन प्रकार्य प्रयोग गर्छौं:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) θ को मान निकाल्न क्याल्कुलेटर प्रयोग गर्नुहोस्, \(\theta \approx 53.13^{\circ}\)
उदाहरण २: \(cos^{−1}(\frac{-1}{2}) \) मूल्याङ्कन गर्नुहोस्
समाधान:
परावर्तन गुण प्रयोग गर्दै: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
प्रतिस्थापन गर्दै \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
उदाहरण ३: \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \) मूल्याङ्कन गर्नुहोस्
समाधान:
पहिचान प्रयोग गर्दै: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
व्युत्क्रम त्रिकोणमितीय प्रकार्यहरूमा , डोमेनले इनपुट मानहरू (x-मानहरू) को सेटलाई जनाउँछ जसको लागि प्रकार्य परिभाषित गरिएको छ, र दायराले प्रकार्यले लिन सक्ने आउटपुट मानहरू (y-मानहरू) को सेटलाई जनाउँछ।
यहाँ छ वटा व्युत्क्रम त्रिकोणमितीय प्रकार्यहरूको डोमेन र दायराहरू छन्:
| प्रकार्य | डोमेन | दायरा |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |