De zes trigonometrische functies zijn sin, cos, tan, cosec, sec en cot.
Laten we proberen \(\angle A\) in de gegeven driehoek te vinden.
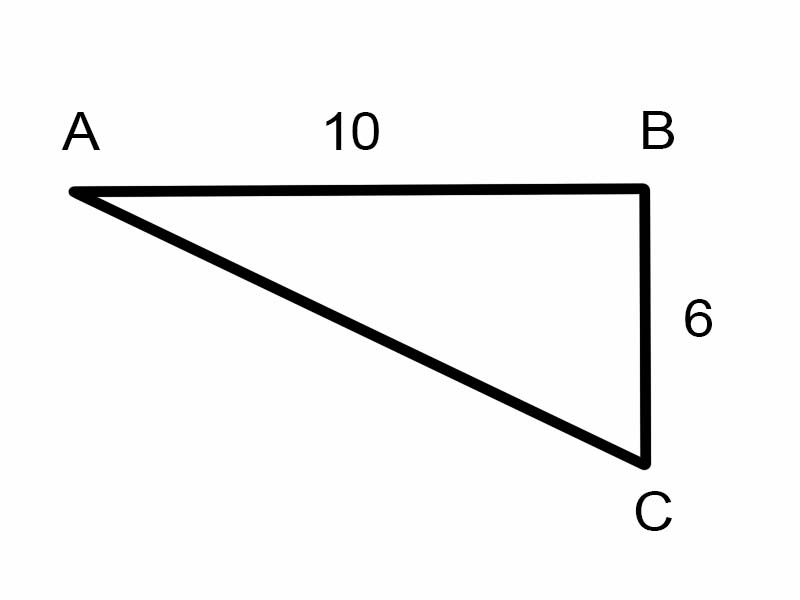
\(\tan A = \frac{6}{10}\)
Maar dit is niet behulpzaam om de maat van \(\angle A\) te vinden
We moeten een nieuw wiskundig hulpmiddel vinden om dit soort problemen op te lossen. Sinus-, cosinus- en tangensfuncties nemen hoeken en geven zijdeverhoudingen. Maar we hebben functies nodig die zijdeverhoudingen nemen en hoeken geven en daarom worden inverse trigonometrische functies geïntroduceerd.
\(\tan A = \frac{6}{10}\)
\( \therefore A = \tan^{-1}\frac{3}{5} = \arctan\frac{3}{5}\)
A = 30,96° [Bereken met de rekenmachine]
Als de lengte van twee zijden bekend is, kunnen hoekmaten worden bepaald met behulp van de inverse trigonometrische functie.
\(\sin^{-1}x \textrm{ of } \arcsin x\) is een inverse sinusfunctie.
\(\cos^{-1}x \textrm{ of } \arccos x \) is de inverse cos-functie.
\(\tan^{-1}x \textrm{ of } \arctan x\) is de inverse tan-functie.
\(\csc^{-1}x \) of arccsc x is de inverse csc-functie.
\(\sec^{-1}x \) of boogseconden x is de inverse sec-functie.
\(cot^{-1}x \) of arccot x is de inverse cot-functie.
In een driehoek zij \(\sin \theta = x\)
⇒ \(\sin \theta = {x \over 1}\) [als \(\sin\theta = \) Loodrecht ∕ Hypotenusa]
We kunnen schrijven als \({x \over 1} = \frac{AB}{AC}\)
\(AC^2 = AB^2 + BC^2\)
⇒ \(1^2 = x^2 + BC^2 \therefore BC^2 = 1 - x^2 \implies BC = \sqrt{(1-x^2)}\)
We kunnen de waarde van trigonometrische verhoudingen afleiden wanneer \(\theta\) als inverse wordt gegeven volgens onderstaande tabel :
1. \(\theta = \sin^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over 1\) | \(\sqrt{1-x^2} \over 1\) | \(x \over \sqrt{1-x^2}\) |
2. \(\theta = \cos^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(\sqrt{1-x^2} \over 1\) | \(x \over 1\) | \(\sqrt{1-x^2} \over x\) |
3. \(\theta = \tan^{-1}x\)
| \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| \(x \over \sqrt{1-x^2}\) | \(1 \over \sqrt{1-x^2}\) | \(x \over 1\) |
\(\sin^{-1}(-x) = - \sin^{-1} x\)
\(\tan^{-1}(-x) = - \tan^{-1} x\)
\(\csc^{-1}(-x) = - \csc^{-1} x\)
\(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
\(\sec^{-1}(-x) = \pi - \sec^{-1} x\)
\(\cot^{-1}(-x) = \pi - \cot^{-1} x\)
\(\sin^{-1}x = \csc^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\cos^{-1}x = \sec^{-1}({1\over x}), x \in [−1,1]−\{0\}\)
\(\tan^{-1}x = \cot^{-1}({1\over x}), x \gt 0\)
\(\cot^{-1}x = \tan^{-1}({1\over x}), x \gt 0\)
\(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\tan^{-1}x + \cot^{-1}x = {\pi \over 2}\)
\(\csc^{-1}x + \sec^{-1}x = {\pi \over 2}\)
Voorbeeld 1: Een ladder leunt tegen een muur en maakt een hoek θ met de grond. De basis van de ladder staat 3 meter van de muur en de ladder is 5 meter lang. Vind θ.
Oplossing:
Omdat we de hypotenusa (5 m) en de aangrenzende zijde (3 m) hebben, gebruiken we de cosinusfunctie:
\(\cos \theta = {3 \over 5}\)
\(\theta = \cos^{-1} ({3 \over 5})\) Gebruik de rekenmachine om de waarde van θ af te leiden, \(\theta \approx 53.13^{\circ}\)
Voorbeeld 2: Evalueer \(cos^{−1}(\frac{-1}{2}) \)
Oplossing:
Gebruik van de reflectie-eigenschap: \(\cos^{-1}(-x) = \pi - \cos^{-1} x\)
Substitueren van \( x=\frac{1}{2} \)
\(\cos^{-1}(\frac{-1}{2}) = \pi - \cos^{-1} (\frac{1}{2})\) ⇒ \(\cos^{-1}(\frac{-1}{2}) = \pi - \frac{\pi}{3} = \frac{2\pi}{3} \)
Voorbeeld 3: Evalueer \(\sin^{-1} 0.6 + \cos^{-1} 0.6 \)
Oplossing:
Gebruik de identiteit: \(\sin^{-1}x + \cos^{-1}x = {\pi \over 2}\)
\(\therefore \sin^{-1} 0.6 + \cos^{-1} 0.6 = \frac {\pi}{2}\)
Bij inverse trigonometrische functies verwijst het domein naar de set invoerwaarden (x-waarden) waarvoor de functie is gedefinieerd, en het bereik verwijst naar de set uitvoerwaarden (y-waarden) die de functie kan aannemen.
Hier zijn de domeinen en bereiken van de zes inverse trigonometrische functies:
| Functie | Domeinbereik | \ |
| \(y = \sin^{-1}x\) | \(-1 \le x \le 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \cos^{-1}x\) | \(-1 \le x \le 1\) | \(0 \le y \le {\pi}\) |
| \(y = \tan^{-1}x\) | \(-\infty \le x \le \infty\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) |
| \(y = \csc^{-1} x\) | \(|x| \ge 1\) | \({-\pi \over 2} \le y \le {\pi \over 2}\) , \(y \ne 0\) |
| \(y = \sec^{-1}x\) | \(|x| \ge 1\) | \(0 \le y \le {\pi}\) , \(y \ne {\pi \over 2}\) |
| \(y = \cot^{-1}x\) | \(-\infty \le x \le \infty\) | \(0 \lt y \lt {\pi}\) |